
 如图,点A是抛物线
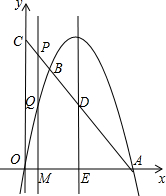
如图,点A是抛物线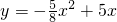 与x轴正半轴的交点,点B在这条抛物线上,且点B的横坐标为2.连接AB并延长交y轴于点C,抛物线的对称轴交AC于点D,交x轴于点E.点P在线段CA上,过点P作x轴的垂线,垂足为点M,交抛物线于点Q.设点P的横坐标为m.
与x轴正半轴的交点,点B在这条抛物线上,且点B的横坐标为2.连接AB并延长交y轴于点C,抛物线的对称轴交AC于点D,交x轴于点E.点P在线段CA上,过点P作x轴的垂线,垂足为点M,交抛物线于点Q.设点P的横坐标为m. x2+5x=0,
x2+5x=0, ×22+5×2=
×22+5×2= ,
, ),
),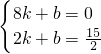 ,
,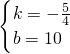 ,
, x+10;
x+10; x2+5x的对称轴为直线x=-
x2+5x的对称轴为直线x=-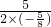 =4,
=4, ×4+10=5,
×4+10=5, x2+5x=5,
x2+5x=5, ,x2=4+2
,x2=4+2 (舍去),
(舍去), ,5);
,5); m+10),点Q(m,-
m+10),点Q(m,- m2+5m),
m2+5m), m+10)-(-
m+10)-(- m2+5m)=
m2+5m)= m2-
m2- m+10,
m+10, m2-
m2- m+10;
m+10; m2+5m)-(-
m2+5m)-(- m+10)=-
m+10)=- m2+
m2+ m-10,
m-10, m2+
m2+ m-10,
m-10, ;
; m2-
m2- m+10的对称轴为直线m=-
m+10的对称轴为直线m=- =5,
=5, >0,
>0, m2+
m2+ m-10的对称轴为直线m=-
m-10的对称轴为直线m=-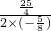 =5,
=5, <0,
<0,

科目:初中数学 来源: 题型:
 如图,点P是抛物线y=x2上位于第一象限内一点,点A(3,0),设点P的坐标为(x,y).
如图,点P是抛物线y=x2上位于第一象限内一点,点A(3,0),设点P的坐标为(x,y).查看答案和解析>>
科目:初中数学 来源:2013届广西贵港市覃塘区初中毕业班第四次教学质量监测试题数学试卷(带解析) 题型:填空题
如图,点B1是抛物线 的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点
的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点 ,则
,则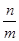 的值是 .
的值是 . 
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市初九年级上学期第二次阶段测数学试卷(解析版) 题型:填空题
有四张正面分别标有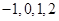 的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中取出一张,将卡片上的数字记为
的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中取出一张,将卡片上的数字记为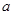 ,不放回,再取出一张,将卡片上的数字记为
,不放回,再取出一张,将卡片上的数字记为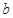 ,设
,设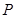 点的坐标为
点的坐标为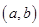 。如图,点
。如图,点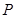 落在抛物线
落在抛物线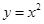 与直线
与直线 所围成的封闭区域内(图中含边界的阴影部分)的概率是
。
所围成的封闭区域内(图中含边界的阴影部分)的概率是
。

查看答案和解析>>
科目:初中数学 来源:2012-2013学年广西贵港市毕业班第四次教学质量监测试卷数学试卷(解析版) 题型:填空题
如图,点B1是抛物线 的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点
的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点 ,则
,则 的值是 .
的值是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com