
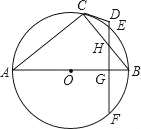
【题目】如图,已知AB是⊙O的直径,BC、EF是⊙O的弦,且EF垂直AB于点G,交BC于点H,CD与FE延长线交于D点,CD=DH.
(1)求证:CD是⊙O的切线;
(2)若H为BC中点,AB=10,EF=8,求CD的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)要求证:DC是圆O的切线,只要证明OC⊥PC即可.
(2)先求出![]() ,CH=
,CH=![]() ,FH=4+
,FH=4+![]() ,进而判断出△DHM∽△BHG,即可得出结论.
,进而判断出△DHM∽△BHG,即可得出结论.
(1)连接OD、OC相交于M,
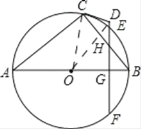
∵∠ACB=90°,CO=AO,
∴∠ACO=∠CAO,∠CAO+∠B=90°,∠B+∠BHG=90°.
∴∠CAO=∠BHG.
∵DC=DH,
∴∠DCH=∠DHC.
∴∠DCH=∠ACO.
∴∠DCH+∠HCO=∠ACO+∠OCH=90°.
∴OC⊥PC.
即DC为切线.
(2)∵AB=10,EF=8,EF垂直AB,
∴EG=4=GF.
∴OG=3,
∴BG=2.
如图1,
在Rt△BFG中,BF=![]()
∵H为BC中点,
∴BH=CH,
设EH=x,则FH=8﹣x,HG=4﹣x,
根据相交弦定理得,BHCH=EHFH,
∴BH2=x(8﹣x),
在Rt△BHG中,BH2﹣HG2=BG2,
∴x(8﹣x)﹣(4﹣x)2=4,
∴x=4+![]() (舍)或x=4﹣
(舍)或x=4﹣![]() ,
,
∴HG=![]() ,BH=CH=
,BH=CH=![]() ,FH=4+
,FH=4+![]() ,
,
过点D作DM⊥CH于M,
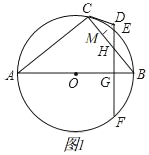
∵CD=HD
∴MH=![]() CH=
CH=![]()
∵∠DHM=∠BHG,∠DMH=∠BGH=90°,
∴△DHM∽△BHG,
∴![]() ,
,
∴![]() ,
,
∴DH=![]() ,
,
∴CD=![]() .
.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
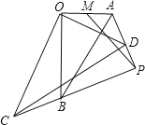
【题目】如图,Rt△AOB∽△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=6,OB=8,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最小值____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
(1)求证:四边形BCFE是菱形;
(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OP与x轴正半轴的夹角为30°,点A是OP上一点,过点A作x轴的垂线与x轴交于点E.△AOE绕着点O逆时针旋转90°后能与△BOC重合,△BOC沿着y轴翻折能与△DOC重合,若点D恰好在抛物线y=x2(x>0)上,则点A的坐标是_____.
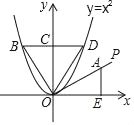
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,小明从原点开始,按照向上平移1个单位长度描点A1,然后向右平移2个单位长度描点A2,然后向上平移2个单位长度描点A3,然后向右平移1个单位长度描点A4,之后重复上述步骤,以此类推进行描点(如图),那么她描出的点A87的坐标是_____.
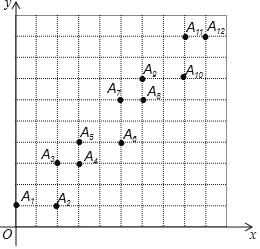
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.
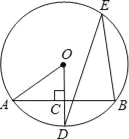
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=(m+1)x+4的图像与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB的面积为4.
(1)则![]() = 及点
= 及点![]() 的坐标为( );
的坐标为( );
(2)过点B作直线BP与![]() 轴的正半轴相交于点P,且OP=4OA,求直线BP的解析式;
轴的正半轴相交于点P,且OP=4OA,求直线BP的解析式;
(3)将一次函数![]() 的图像绕点B顺时针旋转
的图像绕点B顺时针旋转![]() , 求旋转后的对应的函数表达式.
, 求旋转后的对应的函数表达式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com