
【题目】如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.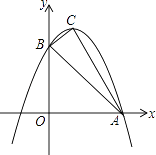
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;
(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.
【答案】
(1)
解:由题意可知,抛物线y=ax2+bx+c与x轴的另一个交点为(﹣1,0),则
 ,
,
解得  .
.
故抛物线的解析式为y=﹣x2+2x+3
(2)
解:依题意:设M点坐标为(0,t),
① 当MA=MB时:
![]()
解得t=0,
故M(0,0);
②当AB=AM时:
![]()
解得t=3(舍去)或t=﹣3,
故M(0,﹣3);
③当AB=BM时,
![]()
解得t=3±3 ![]() ,
,
故M(0,3+3 ![]() )或M(0,3﹣3
)或M(0,3﹣3 ![]() ).
).
所以点M的坐标为:(0,0)、(0,﹣3)、(0,3+3 ![]() )、(0,3﹣3
)、(0,3﹣3 ![]() )
)
(3)
解:平移后的三角形记为△PEF.
设直线AB的解析式为y=kx+b,则
![]() ,
,
解得 ![]() .
.
则直线AB的解析式为y=﹣x+3.
△AOB沿x轴向右平移m个单位长度(0<m<3)得到△PEF,
易得直线EF的解析式为y=﹣x+3+m.
设直线AC的解析式为y=k′x+b′,则
![]() ,
,
解得 ![]() .
.
则直线AC的解析式为y=﹣2x+6.
连结BE,直线BE交AC于G,则G( ![]() ,3).
,3).
在△AOB沿x轴向右平移的过程中.
①当0<m≤ ![]() 时,如图1所示.
时,如图1所示.
设PE交AB于K,EF交AC于M.
则BE=EK=m,PK=PA=3﹣m,
联立 ![]() ,
,
解得 ![]() ,
,
即点M(3﹣m,2m).
故S=S△PEF﹣S△PAK﹣S△AFM
= ![]() PE2﹣
PE2﹣ ![]() PK2﹣
PK2﹣ ![]() AFh
AFh
= ![]() ﹣
﹣ ![]() (3﹣m)2﹣
(3﹣m)2﹣ ![]() m2m
m2m
=﹣ ![]() m2+3m.
m2+3m.
②当 ![]() <m<3时,如图2所示.
<m<3时,如图2所示.
设PE交AB于K,交AC于H.
因为BE=m,所以PK=PA=3﹣m,
又因为直线AC的解析式为y=﹣2x+6,
所以当x=m时,得y=6﹣2m,
所以点H(m,6﹣2m).
故S=S△PAH﹣S△PAK
= ![]() PAPH﹣
PAPH﹣ ![]() PA2
PA2
=﹣ ![]() (3﹣m)(6﹣2m)﹣
(3﹣m)(6﹣2m)﹣ ![]() (3﹣m)2
(3﹣m)2
= ![]() m2﹣3m+
m2﹣3m+ ![]() .
.
综上所述,当0<m≤ ![]() 时,S=﹣
时,S=﹣ ![]() m2+3m;当
m2+3m;当 ![]() <m<3时,S=
<m<3时,S= ![]() m2﹣3m+
m2﹣3m+ ![]() .
.


【解析】(1)根据对称轴可知,抛物线y=ax2+bx+c与x轴的另一个交点为(﹣1,0),根据待定系数法可得抛物线的解析式为y=﹣x2+2x+3.(2)分三种情况:①当MA=MB时;②当AB=AM时;③当AB=BM时;三种情况讨论可得点M的坐标.(3)平移后的三角形记为△PEF.根据待定系数法可得直线AB的解析式为y=﹣x+3.易得AB平移m个单位所得直线EF的解析式为y=﹣x+3+m.根据待定系数法可得直线AC的解析式.连结BE,直线BE交AC于G,则G( ![]() ,3).在△AOB沿x轴向右平移的过程中.根据图象,易知重叠部分面积有两种情况:①当0<m≤
,3).在△AOB沿x轴向右平移的过程中.根据图象,易知重叠部分面积有两种情况:①当0<m≤ ![]() 时;②当
时;②当 ![]() <m<3时;讨论可得用m的代数式表示S.
<m<3时;讨论可得用m的代数式表示S.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】已知AD∥BC,AB⊥AD,点E点F分别在射线AD,射线BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则( )
A.∠AEB+22°=∠DEF
B.1+tan∠ADB=![]()
C.2BC=5CF
D.4cos∠AGB=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,单价30元,试销中发现这种商品每天的销售量夕(件)与每件的销售价![]() (元)满足关系:
(元)满足关系:![]() =100-2
=100-2![]() .若商店每天销售这种商品要获得200元的销售利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?
.若商店每天销售这种商品要获得200元的销售利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题背景:已知,如图1,等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,AB=a,△ABC的面积为S,则有BC=![]() a,S=
a,S=![]() a2.
a2.
(2)迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
①求证:△ADB≌△AEC;
②求∠ADB的度数.
③若AD=2,BD=4,求△ABC的面积.
(3)拓展延伸:如图3,在等腰△ABC中,∠BAC=120°,在∠BAC内作射线AM,点D与点B关于射线AM轴对称,连接CD并延长交AM于点E,AF⊥CD于F,连接AD,BE.
①求∠EAF的度数;
②若CD=5,BD=2,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知五边形OABCD的顶点O在坐标原点,点A在y轴上,点D在x轴上,AB∥x轴,CD∥y轴,动点P从点O出发,以每秒1单位的速度,沿五边形OABCD的边顺时针运动一周,顺次连结P,O,A三点所围成图形的面积为S,点P的运动时间为t秒,S与t之间的函数关系如图2中折线OEFGHI所示.
(1)求证:AB=2;
(2)求五边形OABCD的面积.
(3)求直线BC的函数表达式;
(4)若直线OP把五边形OABCD的面积分成1:3两部分,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展“文明礼仪”演讲比赛,八(1)班、八(2)班派出的5名选手的比赛成绩如图所示.
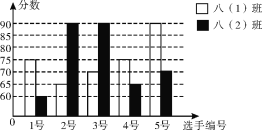
(1)根据上图,完成表格.
平均数 | 中位数 | 方差 | |
八(1)班 | 75 | _______ | _______ |
八(2)班 | 75 | 70 | 160 |
(2)结合两班选手成绩的平均数和方差,分析两个班级参加比赛的选手的成绩.
(3)如果在每班参加比赛的选手中分别选出3人参加决赛,从平均分看,你认为哪个班的实力更强一些?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板按如图所示叠放在一起,若固定![]() ,将
,将![]() 绕着公共顶点
绕着公共顶点![]() ,按顺时针方向旋转
,按顺时针方向旋转![]() 度
度![]() ,当
,当![]() 的一边与
的一边与![]() 的某一边平行时,相应的旋转角
的某一边平行时,相应的旋转角![]() 的度数为_________________。
的度数为_________________。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com