
分析 设每辆车分配的吨数是x,根据按每组人数比预定人数多分配1人,则总数会超过100人和按每组人数比预定人数少分配1人,则总数不够90人按每辆车运送的货物比预定数多1吨,则总数会超过100吨;若按每辆车运送的货物比预定数少1吨,则总数不足90吨,列两个不等式,然后求不等式组的整数解即可.
解答 解:设每辆车分配的吨数是x,
根据题意得$\left\{\begin{array}{l}{8(x+1)>100}\\{8(x-1)<90}\end{array}\right.$,
解得$\frac{23}{2}$<x<$\frac{49}{4}$,
而x为整数,
所以x=12,
即每辆车分配的吨数是12吨.
故答案是:12.
点评 本题考查了一元一次不等式组的应用:一元一次不等式组的应用主要是列一元一次不等式组解应用题,其一般步骤:(1)分析题意,找出不等关系;(2)设未知数,列出不等式组;(3)解不等式组;
(4)从不等式组解集中找出符合题意的答案;(5)作答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
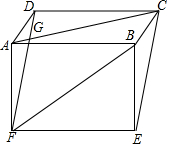 已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G.
已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
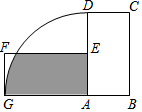 如图,将矩形ABCD绕点A逆时针旋转90°至矩形AEFG,点D的旋转路径为$\widehat{DG}$,若AB=1,BC=2,则阴影部分的面积为( )
如图,将矩形ABCD绕点A逆时针旋转90°至矩形AEFG,点D的旋转路径为$\widehat{DG}$,若AB=1,BC=2,则阴影部分的面积为( )| A. | $\frac{π}{3}$+$\frac{\sqrt{3}}{2}$ | B. | 1+$\frac{\sqrt{3}}{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com