
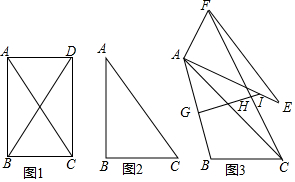
分析 (1)①当n=90°时,图象如图所示.②如图1中,作HM⊥BF于M.设CB=AD=AF=a,AB=b,首先证明MG=MH=$\frac{1}{2}$a,推出∠AGI=45°即可证明.
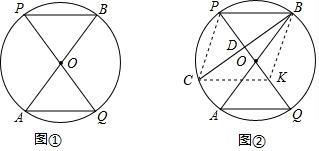
(2)结论仍然成立.如图2中,连接FB、DF,作FN⊥BC于N,交AD于K,作HM⊥AB于M,交BF于O,交FN于Q,作GP⊥FN于P,连接OG、OP,作OJ⊥GP于J.
首先证明△FKD∽△PQH,推出∠FDK=∠QHP,再证明∠QHP=∠AGH,推出∠AIG=∠AFD=∠AGI,即可解决问题.
解答 (1)①解:当n=90°时,图象如图所示.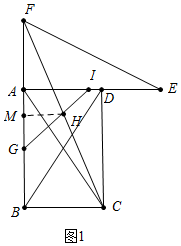
②证明:如图1中,作HM⊥BF于M.设CB=AD=AF=a,AB=b,
∵FH=HC,HM∥BC,
∴FM=BM=$\frac{a+b}{2}$,
∴HM=$\frac{1}{2}$a,
∵BG=$\frac{1}{2}$AB=$\frac{1}{2}$b,
∴MG=BM-GB=$\frac{1}{2}$(a+b)-$\frac{1}{2}$b=$\frac{1}{2}$a,
∴MG=MH,
∴∠MGH=∠MHG=45°,
∵∠GAI=90°,
∴∠AGI=∠AIG=45°,
∴AG=AI,
∵AB=AE,AG=GB,
∴AI=IE.
(2)解:结论仍然成立.理由如下,
如图2中,连接FB、DF,作FN⊥BC于N,交AD于K,作HM⊥AB于M,交BF于O,交FN于Q,作GP⊥FN于P,连接OG、OP,作OJ⊥GP于J.
∵HM∥BC,FH=HC,
∴FQ=QN,FO=OB,
∵AG=BG,
∴AF=2OG,BN=2OQ=2OM,CN=DK=2QI,PK=PN,设AB=m,PQ=n,
∵FQ=QN=$\frac{m}{2}$+n,KQ=$\frac{m}{2}$-n,FK=FQ-KQ=$\frac{m}{2}$+n-($\frac{m}{2}-n$)=2n,
∴FK=2PQ,
∴$\frac{KD}{QI}$=$\frac{KF}{PQ}$=2,∵∠FKD=∠PQH=90°,
∴△FKD∽△PQH,
∴∠FDK=∠QHP,
∵FO=OB,FH=HC,
∴BC=2OH,∵AF=BC=2OG,
∴OH=OG,易证OG=PO,
∴OG=OP=OH,以O为圆心OH为半径作圆,
∵OJ⊥GP,OG=OP,
∴∠GOJ=∠POJ=∠OGM=∠GHP,
∵OG=OH,
∴∠OHG=∠OGH,
∵∠QHP=∠OHG+∠GHP=∠OGH+∠OGM=∠AGH,
∴∠AGH=∠ADF,
∵∠FAD=∠GAH(旋转角相等),
∵AD=AF,
∴∠ADF=∠AFD,
∵∠FAD+∠ADF+∠AFD=180°,∠GAI+∠AGI+∠AIG=180°,
∴∠AIG=∠AFD=∠AGI,
∴AI=AG,
∵AE=AB,AG=GB,
∴AI=IE.
点评 本题考查四边形综合题、旋转变换、矩形的性质、三角形中位线定理、等腰三角形的判定和性质等知识,解题的关键是学会利用参数解决问题,体现了数形结合的数学思想,本题辅助线比较多,发现△FKD∽△PQH,是解题的突破点,属于竞赛题.


科目:初中数学 来源: 题型:解答题
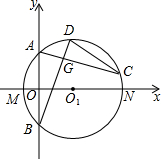 如图,在平面直角坐标系中,直线y=2x+4交x轴于点M,交y轴于点A,过A,M两点的⊙O1的圆心O1在x轴上,交x轴于另一点N,交y轴于另一点B,D,C为优弧$\widehat{AB}$上两动点,且AC⊥BD交BD于G,延长OG交CD于H.
如图,在平面直角坐标系中,直线y=2x+4交x轴于点M,交y轴于点A,过A,M两点的⊙O1的圆心O1在x轴上,交x轴于另一点N,交y轴于另一点B,D,C为优弧$\widehat{AB}$上两动点,且AC⊥BD交BD于G,延长OG交CD于H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙M与x轴交于A、B两点,与y轴切于点C,且OA,OB的长是方程x2-4x+3=0的解.
如图,⊙M与x轴交于A、B两点,与y轴切于点C,且OA,OB的长是方程x2-4x+3=0的解.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系内,梯形OABC的顶点坐标分别是:A(3,4),B(8,4),C(11,0),点P(t,0)是线段OC上一点,设四边形ABCP的面积为S.
如图,在平面直角坐标系内,梯形OABC的顶点坐标分别是:A(3,4),B(8,4),C(11,0),点P(t,0)是线段OC上一点,设四边形ABCP的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | SAS | B. | AAS | C. | ASA | D. | SSS |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com