
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2 ![]() .
.
以上结论中,你认为正确的有 . (填序号)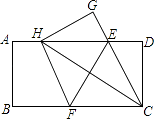
【答案】①③④
【解析】解:∵FH与CG,EH与CF都是矩形ABCD的对边AD、BC的一部分,
∴FH∥CG,EH∥CF,
∴四边形CFHE是平行四边形,
由翻折的性质得,CF=FH,
∴四边形CFHE是菱形,(故①正确);
∴∠BCH=∠ECH,
∴只有∠DCE=30°时EC平分∠DCH,(故②错误);
点H与点A重合时,设BF=x,则AF=FC=8﹣x,
在Rt△ABF中,AB2+BF2=AF2 ,
即42+x2=(8﹣x)2 ,
解得x=3,
点G与点D重合时,CF=CD=4,
∴BF=4,
∴线段BF的取值范围为3≤BF≤4,(故③正确);
过点F作FM⊥AD于M,
则ME=(8﹣3)﹣3=2,
由勾股定理得,
EF= ![]() =
= ![]() =2
=2 ![]() ,(故④正确);
,(故④正确);
综上所述,结论正确的有①③④共3个,
故答案为①③④.
①先判断出四边形CFHE是平行四边形,再根据翻折的性质可得CF=FH,然后根据邻边相等的平行四边形是菱形证明,判断出①正确;②根据菱形的对角线平分一组对角线可得∠BCH=∠ECH,然后求出只有∠DCE=30°时EC平分∠DCH,判断出②错误;③点H与点A重合时,设BF=x,表示出AF=FC=8﹣x,利用勾股定理列出方程求解得到BF的最小值,点G与点D重合时,CF=CD,求出BF=4,然后写出BF的取值范围,判断出③正确;④过点F作FM⊥AD于M,求出ME,再利用勾股定理列式求解得到EF,判断出④正确.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有五人五钱,令上二人所得与下三人等.问各得几何?”其意思为:“现有甲乙丙丁戊五人依次差值等额分五钱,要使甲乙两人所得的钱与丙丁戊三人所得的钱相等,问每人各得多少钱?”根据题意,乙得( )
A.![]() 钱
钱
B.![]() 钱
钱
C.1钱
D.![]() 钱
钱
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旭日商场销售A,B两种品牌的钢琴,这两种钢琴的进价和售价如下表所示:
A | B | |
进价(万元/.套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种钢琴若干套,共需66万元,全部销售后可获毛利润9万元.(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进A,B两种品牌的钢琴各多少套?
(2)通过市场调查,该商场决定在原计划的基础上,减少A种钢琴的购进数量,增加B种钢琴的购进数量,已知B种钢琴增加的数量是A种钢琴减少数量的1.5倍,若用于购进这两种钢琴的总资金不超过69万元,问A种钢琴购进数量至多或减少多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地的铁路路程约为615千米,高铁速度为300千米/小时,直达;动车速度为200千米/小时,行驶180千米后,中途要停靠徐州10分钟,若动车先出发半小时,两车与甲地之间的距离y(千米)与动车行驶时间x(小时)之间的函数图象为( )
A.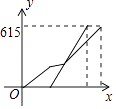
B.
C.
D.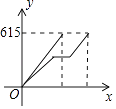
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游风景区出售一种纪念品,该纪念品的成本为12元/个,这种纪念品的销售价格为x(元/个)与每天的销售数量y(个)之间的函数关系如图所示. 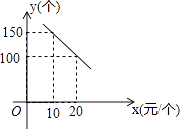
(1)求y与x之间的函数关系式;
(2)销售价格定为多少时,每天可以获得最大利润?并求出最大利润.
(3)“十一”期间,游客数量大幅增加,若按八折促销该纪念品,预计每天的销售数量可增加200%,为获得最大利润,“十一”假期该纪念品打八折后售价为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在△ABC的内部且DB=DC,点E,F在△ABC的外部,FB=FA,EA=EC,∠FBA=∠DBC=∠ECA.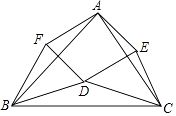
(1)①填空:△ACE∽∽;
(2)求证:△CDE∽△CBA;
(3)求证:△FBD≌△EDC;
(4)若点D在∠BAC的平分线上,判断四边形AFDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,AB⊥BD,CD⊥BD,AP⊥PC,垂足分别为B、P、D,且三个垂足在同一直线上,我们把这样的图形叫“三垂图”.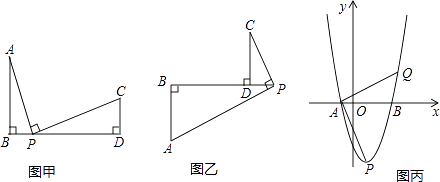
(1)证明:ABCD=PBPD.
(2)如图乙,也是一个“三垂图”,上述结论成立吗?请说明理由.
(3)已知抛物线与x轴交于点A(﹣1,0),B(3,0),与y轴交于点(0,﹣3),顶点为P,如图丙所示,若Q是抛物线上异于A、B、P的点,使得∠QAP=90°,求Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一直角坐标系中,直线y=﹣x+3与y=3x﹣5相交于C点,分别与x轴交于A、B两点.P、Q分别为直线y=﹣x+3与y=3x﹣5上的点.
(1)求△ABC的面积;
(2)若P、Q关于原点成中心对称,求P点的坐标;
(3)若△QPC≌△ABC,求Q点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com