
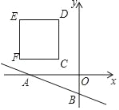
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x﹣1分别交x轴、y轴于点A、B,在第二象限内有一边长为2的正方形CDEF,已知C(﹣1,1),若动点P从C出发以每秒1个单位的速度沿着正方形CDEF的边逆时针运动一周(到达C点后停止运动),设P点运动的时间为t秒.
x﹣1分别交x轴、y轴于点A、B,在第二象限内有一边长为2的正方形CDEF,已知C(﹣1,1),若动点P从C出发以每秒1个单位的速度沿着正方形CDEF的边逆时针运动一周(到达C点后停止运动),设P点运动的时间为t秒.
(1)是否存在t,使得以P为圆心,![]() 为半径的圆与直线AB相切?若存在,求出所有t的值;若存在,请说明理由.
为半径的圆与直线AB相切?若存在,求出所有t的值;若存在,请说明理由.
(2)在点P运动的同时,直线AB以每秒1个单位的速度向右作匀速运动(与点P同时停止)是否存在t,使得以P为圆心,![]() 为半径的圆与平移后的直线A′B′相切?请直接写出所有t的值.
为半径的圆与平移后的直线A′B′相切?请直接写出所有t的值.
【答案】(1)满足条件的t的值为1或4.(2)满足条件的t的值为![]() 或
或![]() 或
或![]() .
.
【解析】
(1) 设存在点P.作PH⊥AB,PM⊥x轴交AB于Q,可证△PHQ∽△AOB,可得PQ=![]() ,分点P在CD上时,与当点P在DE上时讨论,可得t的值;
,分点P在CD上时,与当点P在DE上时讨论,可得t的值;
(2)由题意平移后可得直线A′B′的解析式为,作PH⊥A′B′,PM⊥x轴交A′B′于Q.当PH=![]()
![]() 时,同法可得PQ=
时,同法可得PQ=![]() ,分①当点P在CD上时,②当点P在DE上时,
,分①当点P在CD上时,②当点P在DE上时,
③当点P在EF上时,三种情况讨论,可的t的值.
解:(1)假设存在点P.作PH⊥AB,PM⊥x轴交AB于Q.

∵PQ∥y轴,
∴∠OBA=∠PQH,
∵∠AOB=∠PHQ=Rt∠,
∴△PHQ∽△AOB,
∴![]() =
=![]() ,
,
∵A(﹣1,2)或(﹣3,3),PH=![]() ,
,
∴AO=2,AB=![]() ,
,
∴PQ=![]() ,
,
①当点P在CD上时,t+1+![]() =
=![]() ,解得t=1,
,解得t=1,
②当点P在DE上时,3﹣[﹣![]() (1﹣t)﹣1]=
(1﹣t)﹣1]=![]() ,解得t=4,此时点P与E重合.
,解得t=4,此时点P与E重合.
综上所述,满足条件的t的值为1或4.
(2)由题意平移后的直线A′B′的解析式为y=﹣![]() x﹣1+
x﹣1+![]() ,
,
作PH⊥A′B′,PM⊥x轴交A′B′于Q.
当PH=![]()
![]() 时,同法可得PQ=
时,同法可得PQ=![]() ,
,
①当点P在CD上时,1+t﹣(![]() ﹣1+
﹣1+![]() )=
)=![]() ,解得t=
,解得t=![]() ,
,
②当点P在DE上时,3﹣[﹣![]() (1﹣t)﹣1+
(1﹣t)﹣1+![]() ]=
]=![]() ,解得t=
,解得t=![]() ,
,
③当点P在EF上时,![]() ﹣1+
﹣1+![]() ﹣(6﹣t+1)=
﹣(6﹣t+1)=![]() ,解得t=
,解得t=![]() ,
,
综上所述,满足条件的t的值为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读下列材料,解决问题:
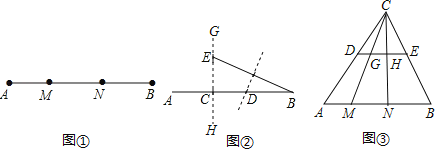
学习了勾股定理后我们知道:直角三角形两条直角边的平方和等于斜边的平方.根据勾股定理我们定义:如图①,点M、N是线段AB上两点,如果线段AM、MN、NB能构成直角三角形,则称点M、N是线段AB的勾股点
解决问题
(1)在图①中,如果AM=2,MN=3,则NB= .
(2)如图②,已知点C是线段AB上一定点(AC<BC),在线段AB上求作一点D,使得C、D是线段AB的勾股点.李玉同学是这样做的:过点C作直线GH⊥AB,在GH上截取CE=AC,连接BE,作BE的垂直平分线交AB于点D,则C、D是线段AB的勾股点你认为李玉同学的做法对吗?请说明理由
(3)如图③,DE是△ABC的中位线,M、N是AB边的勾股点(AM<MN<NB),连接CM、CN分别交DE于点G、H求证:G、H是线段DE的勾股点.
查看答案和解析>>
科目:初中数学 来源: 题型:
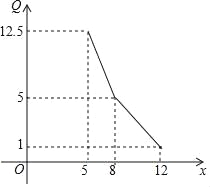
【题目】某专卖店经市场调查得知,一种商品的月销售量 Q(单位:吨)与销售价格 x(单位:万元/吨)的关系可用下图中的折线表示.
(1)写出月销售量 Q 关于销售价格 x 的关系;
(2)如果该商品的进价为 5 万元/吨,除去进货成本外,专卖店销售该商品每月的固定成本为 10 万元,问该商品 每吨定价多少万元时,销售该商品的月利润最大?并求月利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
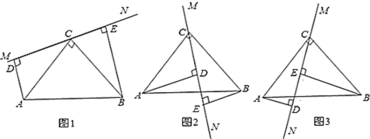
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,且
,且![]() 于点
于点![]() ,
,![]() 于点
于点![]() .易得
.易得![]() (不需要证明).
(不需要证明).
(1)当直线![]() 绕点
绕点![]() 旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时
旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(2)当直线![]() 绕点
绕点![]() 旋转到图3的位置时,其余条件不变,请直接写出此时
旋转到图3的位置时,其余条件不变,请直接写出此时![]() 之间的数量关系(不需要证明).
之间的数量关系(不需要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请用图形变换(对称、平移或旋转)解决下列各题:
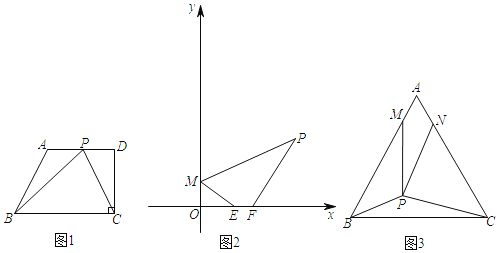
(1)如图1,在四边形ABCD中,AD∥BC,CD⊥BC,∠ABC=60°,AD=8,BC=12,若P是边AD上的任意一点,则△BPC周长的最小值为 .
(2)如图2,已知M(0,1)、P(2+![]() ,3)、E(a,0)、F(a+1,0),问a为何值时,四边形PMEF的周长最小?
,3)、E(a,0)、F(a+1,0),问a为何值时,四边形PMEF的周长最小?
(3)如图3,P为等边△ABC内一点,且PB=2,PC=3,∠BPC=150°,M、N为边AB、AC上的动点,且AM=AN,请直接写出PM+PN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
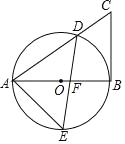
【题目】如图,AB是⊙O的直径,弦DE交AB于点F,⊙O的切线BC与AD的延长线交于点C,连接AE.
(1)试判断∠AED与∠C的数量关系,并说明理由;
(2)若AD=3,∠C=60°,点E是半圆AB的中点,则线段AE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年计划生产玉米和小麦共200吨.采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%.该农场去年实际生产玉米、小麦各多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com