
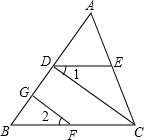
 如图,已知FG⊥AB,CD⊥AB,垂足分别为G、D,∠1=∠2,
如图,已知FG⊥AB,CD⊥AB,垂足分别为G、D,∠1=∠2,分析 由FG⊥AB,CD⊥AB,得到∠FGB=∠CDB=90°,根据平行线的判定和性质得到∠2=∠BCD 由等量代换得到∠1=∠BCD,证出DE∥BC,从而证得结论.
解答 证明:∵FG⊥AB,CD⊥AB,垂足分别为G、D(已知)
∴∠FGB=∠CDB=90°( 垂直的定义),
∴GF∥CD ( 同位角相等,两直线平行).
∵GF∥CD(已证)
∴∠2=∠BCD ( 两直线平行,同位角相等)
又∵∠1=∠2(已知),
∴∠1=∠BCD ( 等量代换),
∴DE∥BC,(内错角相等,两直线平行)
∴∠CED+∠ACB=180.(两直线平行,同旁内角互补)
故答案为:垂直的定义;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;DE∥BC;内错角相等,两直线平行;两直线平行,同旁内角互补.
点评 本题考查了平行线的判定与性质,属于基础题,关键是正确利用平行线的性质与判定定理证明.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
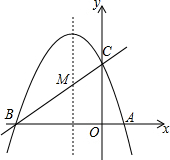 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com