
 如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据全等三角形的性质以及线段垂直平分线的性质,即可得出AM=MC+AD;根据△ABG∽△ADE,且AB<BC,即可得出BG<DE,再根据AM=GM=BG+BM,即可得出AM=DE+BM不成立;根据ME⊥FF,EC⊥MF,运用射影定理即可得出EC2=CM×CF,据此可得DE2=AD•CM成立;根据N不是AM的中点,可得点N不是△ABM的外心.
解答 解:∵E为CD边的中点,
∴DE=CE,
又∵∠D=∠ECF=90°,∠AED=∠FEC,
∴△ADE≌△FCE,
∴AD=CF,AE=FE,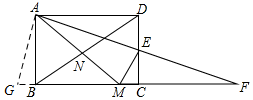
又∵ME⊥AF,
∴ME垂直平分AF,
∴AM=MF=MC+CF,
∴AM=MC+AD,故①正确;
如图,延长CB至G,使得∠BAG=∠DAE,
由AM=MF,AD∥BF,可得∠DAE=∠F=∠EAM,
可设∠BAG=∠DAE=∠EAM=α,∠BAM=β,则∠AED=∠EAB=∠GAM=α+β,
由∠BAG=∠DAE,∠ABG=∠ADE=90°,可得△ABG∽△ADE,
∴∠G=∠AED=α+β,
∴∠G=∠GAM,
∴AM=GM=BG+BM,
由△ABG∽△ADE,可得$\frac{BG}{DE}$=$\frac{AB}{AD}$,
而AB<BC=AD,
∴BG<DE,
∴BG+BM<DE+BM,
即AM<DE+BM,
∴AM=DE+BM不成立,故②错误;
∵ME⊥FF,EC⊥MF,
∴EC2=CM×CF,
又∵EC=DE,AD=CF,
∴DE2=AD•CM,故③正确;
∵∠ABM=90°,
∴AM是△ABM的外接圆的直径,
∵BM<AD,
∴当BM∥AD时,$\frac{MN}{AN}$=$\frac{BM}{AD}$<1,
∴N不是AM的中点,
∴点N不是△ABM的外心,故④错误.
综上所述,正确的结论有2个,
故选:B.
点评 本题主要考查了相似三角形的判定与性质,全等三角形的判定与性质,矩形的性质以及旋转的性质的综合应用,解决问题的关键是运用全等三角形的对应边相等以及相似三角形的对应边成比例进行推导,解题时注意:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心,故外心到三角形三个顶点的距离相等.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).
某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).| 分组/元 | 频 数 | 频 率 |
| 1000<x<1200 | 3 | 0.060 |
| 1200<x<1400 | 12 | 0.240 |
| 1400<x<1600 | 18 | 0.360 |
| 1600<x<1800 | a | 0.200 |
| 1800<x<2000 | 5 | b |
| 2000<x<2200 | 2 | 0.040 |
| 合计 | 50 | 1.000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如
如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如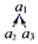 ,表示a1=a2+a3,则a1的最小值为( )
,表示a1=a2+a3,则a1的最小值为( )| A. | 32 | B. | 36 | C. | 38 | D. | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com