练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，正六边形ABCDEF的内切圆和外接圆半径之比为_________.

    【解析】如图所示， 连接BE，AD相交于点O，点O即是六边形ABCDEF内切圆和外接圆的圆心; 过点O作OH⊥AB于点H. ∵六边形ABCDEF为正六边形， ∴∠AOB=360°÷6=60°， ∵OA=OB, ∴△OAB是等边三角形， ∴∠OAB=60°, ∴ .
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省东部分校2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    若将分式中的a与b的值都扩大为原来的2倍，则这个分式的值将( )

    A. 扩大为原来的2倍 B. 分式的值不变 C. 缩小为原来的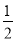 D. 缩小为原来的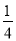

    C 【解析】试题解析：分别用2a和2b去代换原分式中的a和b， 原式=， 可见新分式是原分式的倍． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：江西省萍乡市2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    某公交车原坐有22人，经过4个站点时，上下车情况记录如下（上车为正，下车为负）：+4，-8，-5，+6，-3，+2，+1，-7．则车上还有_____ 人．

    12 【解析】试题解析：根据题意可得：上车为正，下车为负，故车上还有：22+4?8?5+6?3+2+1?7=12人. 故答案为：12.

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型：解答题

    在平面直角坐标系xOy中，抛物线交y轴于点A，交直线x=6于点B.

    （1）填空：抛物线的对称轴为x=_________，点B的纵坐标为__________（用含a的代数式表示）；

    （2）若直线AB与x轴正方向所夹的角为45°时，抛物线在x轴上方，求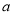的值；

    （3）记抛物线在A、B之间的部分为图像G（包含A、B两点），若对于图像G上任意一点，总有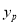≤3，求a的取值范围.

    （1）； ；（2）a=；（3）a≥或a<0． 【解析】(1). ;; （2） ; (3) 或a<0. 试题分析：（1）①根据抛物线的对称轴为直线，代入数据即可得出结论；②把x=6代入直线即可求出点B的纵坐标； （2）根据直线AB与x轴正方向所夹的角为45°，列方程-30a2+36a+3=6+3求出a的值； （3）分a＞0及a＜0两种情况考虑，依照题意画出函数图象，利用数形结...

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型：解答题

    先化简，再求值： ，其中a=－2．

    【解析】试题分析：本题考查了分式的化简求值，先把除法转化为乘法，并把分子、分母分解因式约分化简，再计算分式的加减，最后代入求值即可. = = =. 当a=－2时， 原式=.

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型：填空题

    上海世博会的主题馆与中国馆利用太阳能发电，年发电量可达2840000度．2840000用科学记数法可表示为

    84×106 【解析】2.84×106 较大的数保留有效数字需要用科学记数法来表示．用科学记数法保留有效数字，要在标准形式a×10n中a的部分保留，从左边第一个不为0的数字数起，需要保留几位就数几位，然后根据四舍五入的原理进行取舍． 【解析】 2 840 000=2.84×106．

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型：单选题

    －2018的倒数是（ ）

    A. 2018 B. C. D. －2018

    B 【解析】∵乘积为1的两个数互为倒数， ∴－2018的倒数是. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2017-2018学年七年级上学期期末模四考试数学试卷 题型：填空题

    －0.5的相反数的倒数是__________．

    2 【解析】-0.5的相反数是0.5，0.5的倒数是2， 故答案为：2.

    查看答案和解析>>

    科目：初中数学 来源：北京市延庆区2017-2018学年第一学期八年级期末数学试卷 题型：解答题

    如图-1，△ABC和△DEC都是等腰直角三角形，∠ACB=∠DCE=90°，E在线段AC上，连接AD，BE的延长线交AD于F．

    （1）猜想线段BE，AD的数量关系和位置关系：________________________（不必证明）；

    （2）当点E为△ABC内部一点时，使点D和点E分别在AC的两侧，其它条件不变．

    ① 请你在图-2中补全图形；

    ②（1）中结论成立吗？若成立，请证明；若不成立，请说明理由．

    （1）BE=AD ；BE⊥AD；（2）①答案见解析；②成立 【解析】（1）先通过SAS证△BCE和△ACD全等，再根据全等三角形的性质即可得出BE，AD的数量关系和位置关系； （2）按要求画图所，按（1）的证明思路即可进行证明. 【解析】 （1）∵△ABC和△DEC都是等腰直角三角形，且∠ACB=∠DCE=90°， ∴BC=AC,CE=CD, ∴△BCE≌△ACD(...

    查看答案和解析>>

    同步练习册答案