
【题目】如图,在平面直角坐标系中,函数y= ![]() (x>0,k是常数)的图象经过A(2,6),B(m,n),其中m>2.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连结AD,DC,CB.
(x>0,k是常数)的图象经过A(2,6),B(m,n),其中m>2.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连结AD,DC,CB.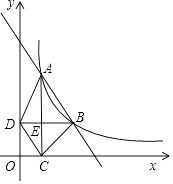
(1)若△ABD的面积为3,求k的值和直线AB的解析式;
(2)求证: ![]() =
= ![]() ;
;
(3)若AD∥BC,求点B的坐标.
【答案】
(1)
解:∵函数y= ![]() (x>0,k是常数)的图象经过A(2,6),
(x>0,k是常数)的图象经过A(2,6),
∴k=2×6=12,
∵B(m,n),其中m>2.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,
∴mn=12①,BD=m,AE=6﹣n,
∵△ABD的面积为3,
∴ ![]() BDAE=3,
BDAE=3,
∴ ![]() m(6﹣n)=3②,
m(6﹣n)=3②,
联立①②得,m=3,n=4,
∴B(3,4);
设直线AB的解析式为y=kx+b(k≠0),
则 ![]() ,
,
∴ ![]() ,
,
∴直线AB的解析式为y=﹣2x+10
(2)
证明:∵A(2,6),B(m,n),
∴BE=m﹣2,CE=n,DE=2,AE=6﹣n,
∴DEAE=2(6﹣n)=12﹣2n,
BECE=n(m﹣2)=mn﹣2n=12﹣2n,
∴DEAE=BECE,
∴ ![]()
(3)
解:由(2)知, ![]() ,
,
∵∠AEB=∠DEC=90°,
∴△DEC∽△BEA,
∴∠CDE=∠ABE
∴AB∥CD,
∵AD∥BC,
∴四边形ADCB是平行四边形.
又∵AC⊥BD,
∴四边形ADCB是菱形,
∴DE=BE,CE=AE.
∴B(4,3)
【解析】(1)先求出k的值,进而得出mn=12,然后利用三角形的面积公式建立方程,联立方程组求解即可;(2)先表示出BE,CE,DE,AE,进而求出BECE和DECE即可得出结论;(3)利用(2)的结论得出△DEC∽△BEA,进而得出AB∥CD,即可得出四边形ADCB是菱形即可得出点B的坐标.


科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,若按图中规律继续下去,则∠1+∠2+…+∠n等于( )
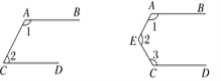

A. n·180° B. 2n·180° C. (n-1)·180° D. (n-1)2·180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到某服装专卖店去做社会调查,了解到该专卖店为了微励营业员的工作积极性,实行“月总收入=基本工资(固定)+计付奖金”的方法计算薪资,并获得如下信息;
营业员 | 小张 | 小王 |
月销售件数 | 200 | 150 |
月总收入/元 | 1400 | 1250 |
销售每件奖励a元,晋业员月基本工资为b元.
(1)列方程组求a,b的值.
(2)假设月销售件数为x,月总收入为y元,请写出y与x的函数关系式,并求出营业员小张上个月总收入是1700元时,小张上个月卖了多少件服装?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC=4.点P是△ABC内的一点,连接PC,以PC为直角边在PC的右上方作等腰直角三角形PCD.连接AD,若AD∥BC,且四边形ABCD的面积为12,则BP的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:
计算代数式![]() (其中x≠0)的值后填入下表.并根据表格所反映出的
(其中x≠0)的值后填入下表.并根据表格所反映出的![]() (其中x≠0)的值与x之间的变化规律进行探究.
(其中x≠0)的值与x之间的变化规律进行探究.
x | …… | 0.25 | 0.5 | 1 | 10 | 100 | 1000 | 10000 | …… |
| …… | …… |
下面是小东计算代数式![]() (其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:
(其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:
x | …… | 0.25 | 0.5 | 1 | 10 | 100 | 1000 | 10000 | …… |
| …… | 2 | 1 |
|
|
|
| …… |
(1)上表是![]() (其中x≠0)与x的几组对应值.直接写出x=10时,求代数式
(其中x≠0)与x的几组对应值.直接写出x=10时,求代数式![]() 的值;
的值;
(2)随着x值的增大,代数式![]() 的值有何变化(回答“增大”或“减少”);
的值有何变化(回答“增大”或“减少”);
(3)当x值无限增大时,代数式![]() 的值无限趋近于一个数,这个数是多少.
的值无限趋近于一个数,这个数是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠B=90°,AB∥DF,AB=3cm,BD=8cm,点C是线段BD上一动点,点E是直线DF上一动点,且始终保持AC⊥CE.
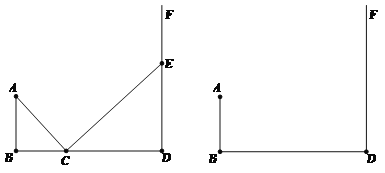
(1)试说明:∠ACB =∠CED
(2)若AC=CE ,试求DE的长
(3)在线段BD的延长线上,是否存在点C,使得AC=CE,若存在,请求出DE的长及△AEC的面积;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED②AC+BE=AB ③∠BDE=∠BAC ④AD平分∠CDE ⑤S△ABD∶S△ACD=AB∶AC,其中正确的有( )
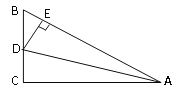
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数的序号填在相应的大括号内:
①﹣17;②π;③﹣|﹣![]() |;④
|;④![]() ;⑤
;⑤![]() ;⑥﹣0.92;⑦
;⑥﹣0.92;⑦![]() ;⑧﹣0.
;⑧﹣0.![]() ;⑨1.2020020002;
;⑨1.2020020002;
(1)正实数{ }
负有理数{ }
无理数{ }
(2)从以上9个数中选取2个有理数,2个无理数,用“+、﹣、×、÷”中的3种不同的运算符号将选出的4个数进行运算(可以用括号),使得计算结果为正整数,列出式子并计算 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com