
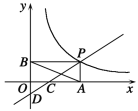
【题目】如图,直线![]() 与x轴、y轴分别交于C、D两点,与双曲线
与x轴、y轴分别交于C、D两点,与双曲线![]() 在第一象限内交于点P,过点P作PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,4)且S△DBP=27.
在第一象限内交于点P,过点P作PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,4)且S△DBP=27.
(1)直接写出直线的解析式_____________,双曲线的解析式____________;
(2)设点Q是直线![]() 上的一点,且满足△DOQ的面积是△COD面积的2倍,请求出点Q的坐标;
上的一点,且满足△DOQ的面积是△COD面积的2倍,请求出点Q的坐标;
【答案】(1)![]() ;
;![]() ;(2)点Q的坐标 (6,2)或(-6,-6).
;(2)点Q的坐标 (6,2)或(-6,-6).
【解析】
(1)令一次函数解析式中x=0,求出对应的y值,确定出D的坐标,得到OD的长,再由已知条件得到OB的长,由OD+OB求出BD的长,在直角三角形BDP中,利用两直角边乘积的一半表示出三角形的面积,将BD及已知的面积代入求出BP的长,确定出P的坐标,由P为一次函数与反比例函数的交点,将P的坐标代入一次函数解析式中求出k的值,确定出一次函数解析式,将P的坐标代入反比例函数解析式中求出m的值,确定出反比例函数解析式;
(2)先求得C的坐标,进而根据S△DOQ=2S△COD,求得MQ=2OC=6,然后分两种情况讨论求得.
(1)∵一次函数y=kx-2的图象交y轴于点D,
∴OD=2.
∵B(0,4),
∴BD=2+4=6,
∵S△DBP=27,
∴![]() BDBP=27,
BDBP=27,
∴BP=9,
∴P(9,4);
把点P的坐标代入y=kx-2得:k=![]() ,
,
∴一次函数的解析式为:y=![]() x-2,
x-2,
把点P的坐标代入y=![]() 得:m=36.
得:m=36.
∴反比例函数的表达式是y=![]() ;
;
(2)∵直线![]() 交x轴于点C,
交x轴于点C,
∴点C的坐标是(3,0),OC=3.
过点Q作QM⊥y轴于点M.
分为以下两种情况:
①当点Q在射线DC上时,
∵△DOQ的面积是△COD面积的2倍,且△DOQ和△COD有共同的底边OD,
∴MQ=2OC=6.
把x=6代入![]() ,得y=2,
,得y=2,
即此时点Q的坐标是(6,2).
②当点Q在射线CD上时,同理可得QM=6,
把x=-6代入![]() ,得y=-6,
,得y=-6,
即此时点Q的坐标是(-6,-6).
∴点Q的坐标 (6,2)或(-6,-6).


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,请用配方法探索有实数根的条件,并推导出求根公式,证明x1x2=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
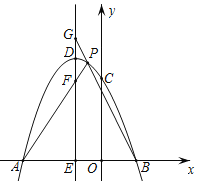
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点(A在B的左侧),且OA=3,OB=1,与y轴交于C(0,3),抛物线的顶点坐标为D(﹣1,4).
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)过点D作直线DE∥y轴,交x轴于点E,点P是抛物线上B、D两点间的一个动点(点P不与B、D两点重合),PA、PB与直线DE分别交于点F、G,当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2014贵州黔东南)黔东南州某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.
(1)求每件甲种、乙种玩具的进价分别是多少元;
(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过20件,超出部分可以享受7折优惠.若购进x(x>0)件甲种玩具需要花费y元,请你求出y与x的函数关系式;
(3)在(2)的条件下,超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,请你帮助超市判断购进哪种玩具省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市购买大件物品都有送货上门服务,那么罗平沃尔玛超市一辆货车从超市出发,向东走了![]() ,到达小明家,继续向东走了
,到达小明家,继续向东走了![]() 到达小红家,又向西走了
到达小红家,又向西走了![]() 到达小英家,最后回到超市.
到达小英家,最后回到超市.
(1)请以超市为原点,以向东为正方向,用1个单位长度表示![]() ,画出数轴.并在数轴上表示出小明家、小红家、小英家的位置;
,画出数轴.并在数轴上表示出小明家、小红家、小英家的位置;
(2)小英家距小明家有多远?
(3)货车一共行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
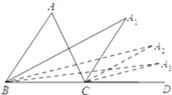
【题目】如图,BA1和CA1分别是△ABC的内角平分线和外角平分线, BA2是∠A1BD的角平分线,CA2 是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3 是∠A2CD的角平分线,若∠A= α,则∠A2019=______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾天气持续笼罩我国大部分地区,困扰着广大市民的生活,口罩市场出现热销,小明的爸爸用12000元购进甲、乙两种型号的口罩在自家商店销售,销售完后共获利2700元,进价和售价如表:

(1)小明爸爸的商店购进甲、乙两种型号口罩各多少袋?
(2)该商店第二次以原价购进甲、乙两种型号口罩,购进甲种型号口罩袋数不变,而购进乙种型号口罩袋数是第一次的2倍,甲种口罩按原售价出售,而效果更好的乙种口罩打折让利销售,若两种型号的口罩全部售完,要使第二次销售活动获利不少于2460元,每袋乙种型号的口罩最多打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
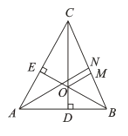
【题目】如图,在△ABC中,CD、BE为高,AN为角平分线,OM平分∠BOC交BC于M.
(1) 若∠BAC=![]() ,求∠BOM;
,求∠BOM;
(2) 求证: OM∥AN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com