
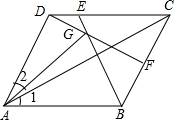
 已知:ABCD为平行四边形,∠1=∠2,AB:AD=k,求BF:DE=?
已知:ABCD为平行四边形,∠1=∠2,AB:AD=k,求BF:DE=? 分析 延长AG交CD于H,AC交BE于Q交DF于O,延长DF交AB的延长线于M.设CF=a,AD=na,由△DAH∽△DCA,得$\frac{DH}{AD}$=$\frac{DA}{DC}$=$\frac{1}{k}$,求出DH=$\frac{na}{k}$,由AD∥CF,DC∥AM,推出△COF∽△AOD,△DOC∽△MOA,推出$\frac{AD}{CF}$=$\frac{OA}{OC}$=$\frac{AM}{CD}$=n,得到AM=kn2a,BM=kna(n-1),由$\frac{DE}{BM}$=$\frac{DG}{GM}$=$\frac{DH}{AM}$,求出DE即可解决问题.
解答 解:延长AG交CD于H,AC交BE于Q交DF于O,延长DF交AB的延长线于M.设CF=a,AD=na,
∵AB=kAD,
∴AB=kna,BF=(n-1)a,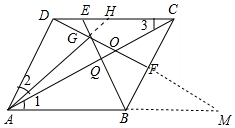
∵AB∥CD,
∴∠1=∠3=∠2,
∵∠ADH=∠ADC,
∴△DAH∽△DCA,
∴$\frac{DH}{AD}$=$\frac{DA}{DC}$=$\frac{1}{k}$,
∴DH=$\frac{na}{k}$,
∵AD∥CF,DC∥AM,
∴△COF∽△AOD,△DOC∽△MOA,
∴$\frac{AD}{CF}$=$\frac{OA}{OC}$=$\frac{AM}{CD}$=n,
∴AM=kn2a,BM=kna(n-1),
∵$\frac{DE}{BM}$=$\frac{DG}{GM}$=$\frac{DH}{AM}$,
∴$\frac{DE}{kna(n-1)}$=$\frac{na}{{k}^{2}{n}^{2}a}$,
∴DE=$\frac{(n-1)a}{k}$,
∴$\frac{BF}{DE}$=$\frac{(n-1)a}{\frac{(n-1)a}{k}}$=k.
点评 本题考查相似三角形的判定和性质、平行四边形的性质、平行线分线段成比例定理等知识,解题的关键是学会利用参数解决问题,题目比较难.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
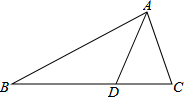 △ABC中,AD是∠BAC的平分线,且AB=AC+CD.若∠BCA=60°,则∠ABC的大小为( )
△ABC中,AD是∠BAC的平分线,且AB=AC+CD.若∠BCA=60°,则∠ABC的大小为( )| A. | 30° | B. | 60° | C. | 80° | D. | 100° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -4 | C. | -7 | D. | -8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
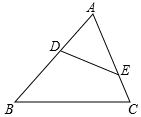 如图,添加下列一个条件,不能使△ADE∽△ACB的是( )
如图,添加下列一个条件,不能使△ADE∽△ACB的是( )| A. | $\frac{AE}{AC}$=$\frac{DE}{BC}$ | B. | ∠AED=∠B | C. | $\frac{AD}{AC}$=$\frac{AE}{AB}$ | D. | ∠ADE=∠C |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com