
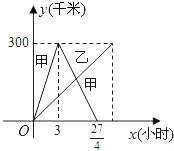
【题目】已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)求甲车离出发地的距离y甲(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)若已知乙车行驶的速度是40千米/小时,求出发后多长时间,两车离各自出发地的距离相等;
(3)在上述条件下,直接写出它们在行驶过程中相遇时的时间.
【答案】(1)y=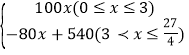 ;(2)出发后
;(2)出发后![]() 小时,两车离各自出发地的距离相等;(3)两车第一次相遇时间为第
小时,两车离各自出发地的距离相等;(3)两车第一次相遇时间为第![]() 小时,第二次相遇时间为第6小时.
小时,第二次相遇时间为第6小时.
【解析】
(1)由图知,该函数关系在不同的时间里表现成不同的关系,需分段表达.当行驶时间小于3时是正比例函数;当行使时间大于3小时小于![]() 小时是一次函数.可根据待定系数法列方程,求函数关系式.
小时是一次函数.可根据待定系数法列方程,求函数关系式.
(2)设出发后a小时,两车离各自出发地的距离相等,列出方程即可解决问题;
(3)两者相向而行,相遇时甲、乙两车行使的距离之和为300千米,列出方程解答,由题意有两次相遇.
(1)当0≤x≤3时,是正比例函数,设为y=kx,
x=3时,y=300,代入解得k=100,所以y=100x;
当3<x≤![]() 时,是一次函数,设为y=kx+b,
时,是一次函数,设为y=kx+b,
代入两点(3,300)、(![]() ,0),得
,0),得![]() 解得
解得![]() ,
,
所以y=540﹣80x.
综合以上得甲车离出发地的距离y与行驶时间x之间的函数关系式 为:y=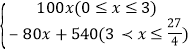 ;
;
(2)设出发后a小时,两车离各自出发地的距离相等.
由题意﹣80a+540=40a,
解得a=![]() s,
s,
答:出发后![]() 小时,两车离各自出发地的距离相等.
小时,两车离各自出发地的距离相等.
(3)由题意有两次相遇.
①当0≤x≤3,100x+40x=300,解得x=![]() ;
;
②当3<x≤![]() 时,(540﹣80x)+40x=300,解得x=6.
时,(540﹣80x)+40x=300,解得x=6.
综上所述,两车第一次相遇时间为第![]() 小时,第二次相遇时间为第6小时.
小时,第二次相遇时间为第6小时.


科目:初中数学 来源: 题型:
【题目】先阅读,后解答:
(1)由根式的性质计算下列式子得:
①![]() =3,②
=3,②![]() ,③
,③![]() ,④
,④![]() =5,⑤
=5,⑤![]() =0.
=0.
由上述计算,请写出![]() 的结果(a为任意实数).
的结果(a为任意实数).
(2)利用(1)中的结论,计算下列问题的结果:
①![]() ;
;
②化简:![]() (x<2).
(x<2).
(3)应用:
若![]() =3,求x的取值范围.
=3,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏在作⊙O的内接正五边形时,先做了如下几个步骤:
(i)作⊙O的两条互相垂直的直径,再作OA的垂直平分线交OA于点M,如图1;
(ii)以M为圆心,BM长为半径作圆弧,交CA于点D,连结BD,如图2.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是( )
A.BD2= ![]() OD
OD
B.BD2= ![]() OD
OD
C.BD2= ![]() OD
OD
D.BD2= ![]() OD
OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校体育组为了了解学生喜欢的体育项目,从全校同学中随机抽取了若干名同学进行调查,每位同学从乒乓球、篮球、羽毛球、排球、跳绳中选择一项最喜欢的项目,并将调查的结果绘制成如下的两幅统计图.根据以上统计图,解答下列问题: 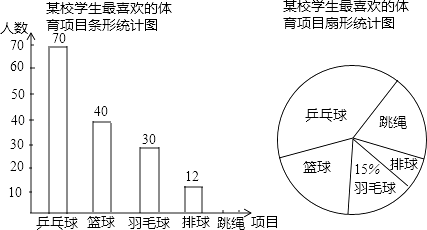
(1)这次被调查的共有多少名同学?并补全条形统计图.
(2)若全校有1200名同学,估计全校最喜欢篮球和排球的共有多少名同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校八年级共有三个班,都参加了学校举行的书法绘画大赛,三个班根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分100分)如下表所示:
决赛成绩(单位:分) | |
八年1班 | 80 86 88 80 88 99 80 74 91 89 |
八年2班 | 85 85 87 97 85 76 88 77 87 88 |
八年3班 | 82 80 78 78 81 96 97 87 92 84 |
解答下列问题:
(1)请填写下表:
平均数(分) | 众数(分) | 中位数(分) | |
八年1班 | 85.5 |
| 87 |
八年2班 | 85.5 | 85 |
|
八年3班 |
| 78 | 83 |
(2)请从以下两个不同的角度对三个班级的决赛成绩进行
①从平均数和众数相结合看(分析哪个班级成绩好些).
②从平均数和中位数相结合看(分析哪个班级成绩好些).
(3)如果在每个班级参加决赛的选手中分别选出3人参加总决赛,你认为哪个班级的实力更强一些?请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
如图![]() ,把
,把![]() 沿直线
沿直线![]() 平行移动线段
平行移动线段![]() 的长度,可以变到
的长度,可以变到![]() 的位置;
的位置;
如图![]() ,以
,以![]() 为轴,把
为轴,把![]() 翻折
翻折![]() ,可以变到
,可以变到![]() 的位置;
的位置;
如图![]() ,以点
,以点![]() 为中心,把
为中心,把![]() 旋转
旋转![]() ,可以变到
,可以变到![]() 的位置.
的位置.
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的.这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
回答下列问题:
①在图![]() 中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使
中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使![]() 变到
变到![]() 的位置;
的位置;
②指图中线段![]() 与
与![]() 之间的关系,为什么?
之间的关系,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节快到了,某市共青团组织以“中学生最喜欢项节日活动”为主题题进行了简单的随机抽样调查,让学生从“郊外踏青、品尝美食、观赏电影、参观室馆”四项活动中选择一项,然后绘制出以下两幅不完整的统计图.请根据图中的信息,回答下列问题: 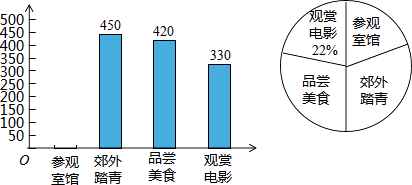
(1)这次抽样调查中共调查了人;扇形统计图中郊外踏青部分的圆心角的度数是°;
(2)请补全条形统计图;
(3)某市有中学生3万人,请估计选择郊外踏青的人数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论正确的是( )
A.x2﹣2是二次二项式
B.单项式﹣x2的系数是1
C.使式子 ![]() 有意义的x的取值范围是x>﹣2
有意义的x的取值范围是x>﹣2
D.若分式 ![]() 的值等于0,则a=±1
的值等于0,则a=±1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°. 
(1)判断△ABC的形状:;
(2)试探究线段PA、PB、PC之间的数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com