
【题目】在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象经过点A(0,﹣4)和B(﹣2,2).
(1)求c的值,并用含a的式子表示b;
(2)当﹣2<x<0时,若二次函数满足y随x的增大而减小,求a的取值范围;
(3)直线AB上有一点C(m,5),将点C向右平移4个单位长度,得到点D,若抛物线与线段CD只有一个公共点,求a的取值范围.
【答案】(1)b=2a﹣3;(2)![]() ≤a<0或0<a≤
≤a<0或0<a≤![]() ;(3)0<a<4或
;(3)0<a<4或![]() .
.
【解析】
(1)把点A(0,﹣4)和B(﹣2,2)分别代入y=ax2+bx+c,即可求解;
(2)当a<0时,依题意抛物线的对称轴需满足![]() ≤﹣2;当a>0时,依题意抛物线的对称轴需满足
≤﹣2;当a>0时,依题意抛物线的对称轴需满足![]() ≥0,即可求解;
≥0,即可求解;
(3)①当a>0时,若抛物线与线段CD只有一个公共点,则抛物线上的点(1,3a﹣7)在D点的下方,即可求解;②当a<0时,若抛物线的顶点在线段CD上,则抛物线与线段只有一个公共点,即可求解.
解:(1)把点A(0,﹣4)和B(﹣2,2)分别代入y=ax2+bx+c中,得
c=﹣4,4a﹣2b+c=2.
∴b=2a﹣3;
(2)当a<0时,依题意抛物线的对称轴需满足![]() ≤﹣2,
≤﹣2,
解得![]() ≤a<0.
≤a<0.
当a>0时,依题意抛物线的对称轴需满足![]() ≥0,
≥0,
解得 0<a≤![]() .
.
∴a的取值范围是![]() ≤a<0或0<a≤
≤a<0或0<a≤![]() ;
;
(3)设直线AB的表达式为:y=mx+n,则![]() ,解得:
,解得:![]() ,
,
故直线AB表达式为y=﹣3x﹣4,把C(m,5)代入得m=﹣3.
∴C(﹣3,5),由平移得D(1,5).
①当a>0时,若抛物线与线段CD只有一个公共点(如图1),
y=ax2+bx+c=ax2+(2a﹣3)﹣4,当x=1时,y=3a﹣7,
则抛物线上的点(1,3a﹣7)在D点的下方,
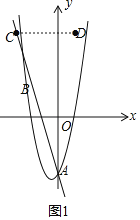
∴a+2a﹣3﹣4<5.
解得a<4.
∴0<a<4;
②当a<0时,若抛物线的顶点在线段CD上,
则抛物线与线段只有一个公共点(如图2),
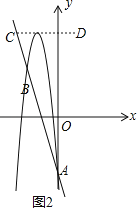
∴![]() .
.
即![]() .
.
解得![]() (舍去)或
(舍去)或![]() .
.
综上,a的取值范围是0<a<4或![]() .
.


科目:初中数学 来源: 题型:
【题目】为提升英语听力及口语技能,小明打算在手机上安装一款英语口语APP辅助练习.他分别从甲、乙、丙三款口语APP中随机选取了1000条网络评价进行对比,统计如下:
等级 评价数量 APP | 五星 | 四星 | 三星 | 二星 | 一星 | 合计 |
甲 | 562 | 286 | 79 | 48 | 25 | 1000 |
乙 | 517 | 393 | 52 | 21 | 17 | 1000 |
丙 | 504 | 210 | 136 | 116 | 34 | 1000 |
(说明:网上对于口语APP的综合评价从高到低依次为五星、四星、三星、二星和一星).
小明选择________(填“甲”、“乙”或“丙”)款英语口语APP,能获得良好口语辅助练习(即评价不低于四星)的可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小石设计的“过直线上一点作这条直线的垂线”的尺规作图过程.
已知:如图1,直线l及直线l上一点P.
求作:直线PQ,使得PQ⊥l.
作法:如图2:
①以点P为圆心,任意长为半径作弧,交直线l于点A,B;
②分别以点A,B为圆心,以大于![]() AB的同样长为半径作弧,两弧在直线l上方交于点Q;
AB的同样长为半径作弧,两弧在直线l上方交于点Q;
③作直线PQ.
所以直线PQ就是所求作的直线.
根据小石设计的尺规作图过程:
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接QA,QB.
∵QA= ,PA= ,
∴PQ⊥l ( )(填推理的依据).
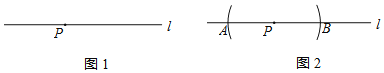
查看答案和解析>>
科目:初中数学 来源: 题型:
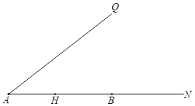
【题目】已知:如图,∠QAN为锐角,H、B分别为射线AN上的点,点H关于射线AQ的对称点为C,连接AC,CB.
(1)依题意补全图;
(2)CB的垂直平分线交AQ于点E,交BC于点F.连接CE,HE,EB.
①求证:△EHB是等腰三角形;
②若AC+AB=![]() AE,求
AE,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宜跟几位同学在某快餐厅吃饭,如图为此快餐厅的菜单.若他们所点的餐食总共为10份盖饭,x杯饮料,y份凉拌菜.
(1)他们点了 份A套餐, 份B套餐, 份C套餐(均用含x或y的代数式表示);
(2)若x=6,且A、B、C套餐均至少点了1份,则最多有 种点餐方案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ABC=60°,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接DF.
(1)求证:△ABF是等边三角形;
(2)若∠CDF=45°,CF=2,求AB的长度.
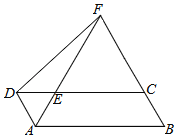
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B是⊙C上的两个点,点P在⊙C的内部.若∠APB为直角,则称∠APB为AB关于⊙C的内直角,特别地,当圆心C在∠APB边(含顶点)上时,称∠APB为AB关于⊙C的最佳内直角.如图1,∠AMB是AB关于⊙C的内直角,∠ANB是AB关于⊙C的最佳内直角.在平面直角坐标系xOy中.
(1)如图2,⊙O的半径为5,A(0,﹣5),B(4,3)是⊙O上两点.
①已知P1(1,0),P2(0,3),P3(﹣2,1),在∠AP1B,∠AP2B,∠AP3B,中,是AB关于⊙O的内直角的是 ;
②若在直线y=2x+b上存在一点P,使得∠APB是AB关于⊙O的内直角,求b的取值范围.
(2)点E是以T(t,0)为圆心,4为半径的圆上一个动点,⊙T与x轴交于点D(点D在点T的右边).现有点M(1,0),N(0,n),对于线段MN上每一点H,都存在点T,使∠DHE是DE关于⊙T的最佳内直角,请直接写出n的最大值,以及n取得最大值时t的取值范围.
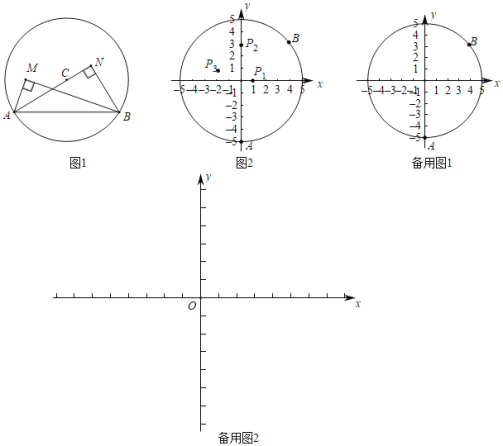
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面内有一点![]() 到
到![]() 的三个顶点的距离分别为
的三个顶点的距离分别为![]() 若有
若有![]() ,则称点
,则称点![]() 为
为![]() 关于点
关于点![]() 的勾股点.
的勾股点.
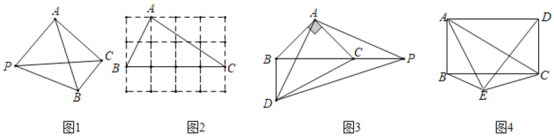
![]() 如图2,在
如图2,在![]() 的方格纸中,每个小正方形的边长均为
的方格纸中,每个小正方形的边长均为![]() 的顶点在格点上,请找出所有的格点
的顶点在格点上,请找出所有的格点![]() ,使点
,使点![]() 为
为![]() 关于点
关于点![]() 的勾股点;
的勾股点;
![]() 如图3,
如图3, ![]() 为等腰直角三角形,
为等腰直角三角形,![]() 是斜边
是斜边![]() 延长线上一点,连接
延长线上一点,连接![]() ,以
,以![]() 为直角边作等腰直角三角形
为直角边作等腰直角三角形 ![]() (点
(点![]() 顺时针排列),
顺时针排列),![]() ,连接
,连接 ![]() 求证:点
求证:点![]() 为
为![]() 关于点
关于点![]() 的勾股点;
的勾股点;
![]() 如图4,点
如图4,点![]() 是矩形
是矩形![]() 外一点,且点
外一点,且点![]() 是
是![]() 关于点
关于点![]() 的勾股点,若
的勾股点,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O交AB于点D,线段BC上有一点P.
(1)当点P在什么位置时,直线DP与⊙O有且只有一个公共点,补全图形并说明理由.
(2)在(1)的条件下,当BP=![]() ,AD=3时,求⊙O半径.
,AD=3时,求⊙O半径.
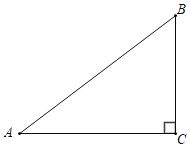
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com