练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．若关于x的一元一次不等式组$\left\{\begin{array}{l}{x-a＞0}\\{2x-2＜1-x}\end{array}\right.$有解，则a的取值范围是a＜1．

    分析 不等式组中两不等式分别求出解集，由不等式组有解确定出a的范围即可．

    解答 解：不等式整理得：$\left\{\begin{array}{l}{x＞a}\\{x＜1}\end{array}\right.$，
    由不等式有解，得到a＜1，
    则a的范围是a＜1，
    故答案为：a＜1

    点评 此题考查了不等式的解集，熟练掌握不等式组取解集的方法是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    15．如图，抛物线y=ax2+bx+c（a≠0）与x轴、y轴分别交于点A（-1，0），B（3，0）、C（0，-3）三点．
    （1）直接写出抛物线的解析式y=x2-2x-3；
    （2）点D（2，m）在抛物线上，连接BC、BD，试问，在对称轴左侧的抛物线上是否存在一点P，满足∠PBC=∠DBC？如果存在，请求出点P点的坐标；如果不存在，请说明理由．
    （3）如图2，在（2）的条件下，将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移，记平移后的三角形为△B′O′C′，在平移过程中，△B′O′C′与△BCD重叠的面积记为S，设平移的时间为t秒（0≤t≤3），试求S与t之间的函数关系式？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．一个扇形的半径为6cm，弧长是4πcm，这个扇形的面积是12πcm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

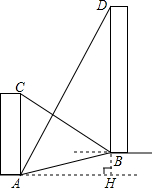    13．如图，AC、BD是一斜坡AB上的两幢楼房，斜坡AB的坡度是$1：2\sqrt{3}$．从点A测得楼BD顶部D处的仰角是60°，从点B测得楼AC顶部C处的仰角是30°，楼BD的自身高度比楼AC高12m．求楼AC与楼BD之间的水平距离．（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．不等式组$\left\{\begin{array}{l}{2-x＞0}\\{2x+3＞1}\end{array}\right.$的解集是-1＜x＜2
    计算：$\sqrt{24}$-$\sqrt{6}$=$\sqrt{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．观察下列等式：
    21=2，22=4，23=8，24=16，25=32，26=64，27=128，…，解答下面问题：2+22+23+24+…+22016-1的末位数字是9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．A、B、C、D、E五张卡片上分别写有tan30°，-2，π，4$\sqrt{5}$，0.010010001五个实数，从中任取一张卡片，则取到的数是无理数的概率为$\frac{3}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

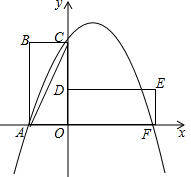
    14．如图，在玲玲家住宅楼CD的前面新建了一个大型商场AB，当光线与地面的夹角是22°时，商场在玲玲家楼上留下高2m的影子CE；而当光线与地面的夹角是45°时，商场楼顶A在地面上的影子F与墙角C有13m的距离（B、F、C在一条直线上）．求商场AB的高度．（参考数据：sin22°≈$\frac{3}{8}$，cos22°≈$\frac{15}{16}$，tan22°≈$\frac{2}{5}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，在平面直角坐标系中，矩形OABC的边OA在x轴的负半轴上，边OC在y轴的正半轴上，且OA=1，tan∠ACB=2，将矩形OABC绕点O按顺时针方向旋转90°后得到矩形ODEF．点A的对应点为点D，点B的对应点为点E，点C的对应点为点F，抛物线y=ax2+bx+2的图象过点A，C，F．
    （1）求抛物线所对应函数的表达式；
    （2）在边DE上是否存在一点M，使得以O，D，M为顶点的三角形与△ODE相似，若存在，求出经过M点的反比例函数的表达式，若不存在，请说明理由；
    （3）在x轴的上方是否存在点P，Q，使以O，F，P，Q为顶点的平行四边形的面积是矩形OABC面积的2倍，且点P在抛物线上，若存在，请求出P，Q两点的坐标；若不能存在，请说明理由；
    （4）在抛物线的对称轴上是否存在一点H，使得HA-HC的值最大，若存在，直接写出点H的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案