
【题目】已知抛物线y=ax2+bx+c 如图所示,直线x=-1是其对称轴,

(1)确定a,b,c, Δ=b2-4ac的符号,
(2)求证:a-b+c>0,
(3)当x取何值时,y>0;当x取何值时y<0.
【答案】(1)a<0,b<0,c>0,b2-4ac>0;
(2)a-b+c>0;
(3)当-3<x<1时y>0 ,∴当x<-3或x>1时,y<0.
【解析】
思路点拨:(1)根据开口方向确定a的符号,根据对称轴的位置确定b的符号,根据抛物线与y轴的交点确定c的符号,根据抛物线与x轴交点的个数确定b2-4ac的符号;
(2)根据图象和x=-1的函数值确定a-b+c与0的关系;
(3)抛物线在x轴上方时y>0;抛物线在x轴下方时y<0.
试题分析:
由抛物线的开口向下,得a<0,由抛物线与y轴的交点在x轴上方,得c>0,
又由![]() <0,∴
<0,∴![]() >0,
>0,
∴a、b同号,由a<0得b<0.
由抛物线与x轴有两个不同的交点,
∴Δ=b2-4ac>0
(2)由抛物线的顶点在x 轴上方,对称轴为x=-1.
∴当x=-1时,y=a-b+c>0
(3)由图象可知:当-3<x<1时y>0 ,
∴当x<-3或x>1时,y<0


科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.
(1)如图1,∠AEE'= °;
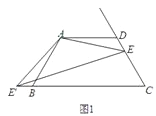
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
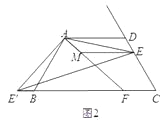
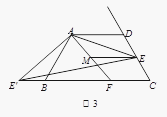
(3)如图3,在(2)的条件下,如果CE=2,AE=![]() ,求ME的长.
,求ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
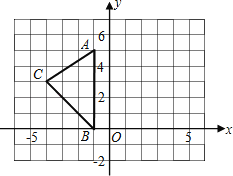
【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积.
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1.
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac,
其中正确的有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是某同学在沙滩上用石子摆成的小房子.观察图形的变化规律,第14个小房子用的石子数量为( )

A. 224B. 250C. 252D. 256
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() .以
.以![]() 为直角边且在
为直角边且在![]() 的上方作等腰直角三角形
的上方作等腰直角三角形![]() .
.
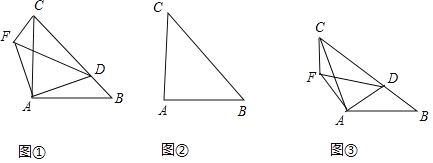
(1)若![]() ,
,![]()
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),试探讨
不重合),试探讨![]() 与
与![]() 的数量关系和位置关系;
的数量关系和位置关系;
②当点![]() 在线段
在线段![]() 的延长线上时,①中的结论是否仍然成立,请在图2中面出相应的图形并说明理由;
的延长线上时,①中的结论是否仍然成立,请在图2中面出相应的图形并说明理由;
(2)如图3,若![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动,试探究
上运动,试探究![]() 与
与![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
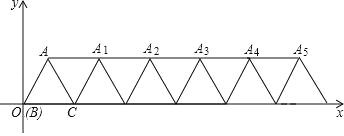
【题目】如图,在平面直角坐标系内,边长为 4 的等边△ABC 的顶点 B 与原点重合,将△ABC 绕顶点 C 顺时针旋转 60°得到△ACA1,将四边形 ABCA1看作一个基本图形,将此基本图形不断复制并平移,请回答:
(1)求点 A的坐标;点 A1的坐标.
(2)求A2018的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)深圳大运会期间,某宾馆有若干间住房,住宿记录提供了如下信息:①7月20日全部住满,一天住宿费收入为3600元;②7月21日有10间房空着,一天住宿费收入为2800元;③该宾馆每间房每天收费标准相同。
【1】(1)求该宾馆共有多少间住房,每间住房每天收费多少元?
【2】(2)通过市场调查发现,每个住房每天的定价每增加10元,就会有一个房间空闲;己知该宾馆空闲房间每天每间费用10元,有游客居住房间每天每间再增加20元的其他费用,问房价定为多少元时,该宾馆一天的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com