
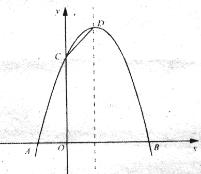
如图,已知抛物线与![]() 轴交于A(-1,0)、B(3,0)两点,与
轴交于A(-1,0)、B(3,0)两点,与![]() 轴交于点C(0,3)。
轴交于点C(0,3)。
(1)求抛物线的解析式;
(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形,若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)若点M是抛物线上一点,以B、C,D、M为顶点的四边形是直角梯形,试求出点M的坐标。
解:(1)∵抛物线与![]() 轴交于点(0,3),
轴交于点(0,3),
∴设抛物线解析式为![]() 。
。
根据题意,得![]() ,解得
,解得![]() 。
。
∴抛物线的解析式为![]() 。
。
(2)存在。
由![]() ,得D点坐标为(1,4),对称轴为
,得D点坐标为(1,4),对称轴为![]() 。
。
①若以CD为底边,则PD=PC,
设P点坐标为![]() ,根据勾股定理,得
,根据勾股定理,得
![]() ,
,
即![]() 。
。
又点P![]() 在抛物线上,
在抛物线上,
∴![]() ,即
,即![]() 。
。
解得![]() 。
。
∵![]() ,应舍去,∴
,应舍去,∴![]() 。
。
![]() 。
。
即点P的坐标为![]() 。
。
②若以CD为一腰,因为点P在对称轴右侧的抛物线上,由抛物线对称性知,
点P与点C关于直线![]() 对称,此时P点坐标为(2,3)。
对称,此时P点坐标为(2,3)。
∴符合条件的点P坐标为![]() 或(2,3)。
或(2,3)。
(3)由B(3,0),C(0,3),D(1,4),根据勾股定理,得
![]() ,
,![]() ,
,![]() 。
。
∴![]()
∴∠BCD=90º,
设对称轴交![]() 轴于点E,过C做CM⊥DE,交抛物线于点M,垂足为F。
轴于点E,过C做CM⊥DE,交抛物线于点M,垂足为F。
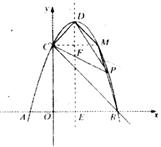
在Rt△DCF中,
∵CF=DF=1,∴∠CDF=45º,
由抛物线的对称性知,
∠CDM=2×45º=90º,点M坐标为(2,3)
∴DM∥BC。
∴四边形BCDM为直角梯形。
由∠BCD=90º及题意可知,
以BC为一底时,顶点M在抛物线上的直角梯形只有上述一种情况;
以CD为一底或以BD为一底,且顶点M在抛物线上的直角梯形均不存在。
综上所述,符合条件的点M的坐标为(2,3)。


科目:初中数学 来源: 题型:
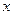 轴交于点
轴交于点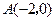 ,
,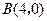 ,与
,与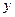 轴交于点
轴交于点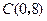 .
.
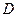 的坐标;
的坐标;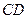 交
交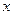 轴于点
轴于点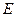 .在线段
.在线段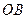 的垂直平分线上是否存在点
的垂直平分线上是否存在点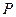 ,使得点
,使得点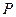 到直线
到直线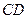 的距离等于点
的距离等于点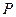 到原点
到原点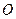 的距离?如果存在,求出点
的距离?如果存在,求出点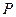 的坐标;如果不存在,请说明理由;
的坐标;如果不存在,请说明理由;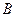 作
作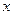 轴的垂线,交直线
轴的垂线,交直线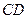 于点
于点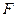 ,将抛物线沿其对称轴平移,使抛物线与线段
,将抛物线沿其对称轴平移,使抛物线与线段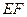 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?查看答案和解析>>
科目:初中数学 来源: 题型:
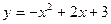 与
与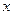 轴的两个交点为A、B,与
轴的两个交点为A、B,与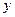 轴交于点C
轴交于点C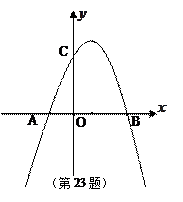
查看答案和解析>>
科目:初中数学 来源:2011年陕西省西安音乐学院初一上学期期末考试数学卷 题型:解答题
如图,已知抛物线与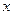 轴交于点
轴交于点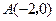 ,
,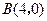 ,与y轴交于点
,与y轴交于点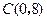 .
.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交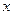 轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源:2011年陕西省西安音乐学院初一上学期期末考试数学卷 题型:解答题
如图,已知抛物线与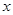 轴交于点
轴交于点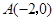 ,
,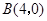 ,与y轴交于点
,与y轴交于点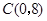 .
.

(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交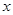 轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源:2010年湖北省黄冈市初二上学期期末数学卷 题型:解答题
如图,已知抛物线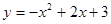 与
与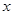 轴的两个交点为A、B,与
轴的两个交点为A、B,与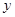 轴交于点C
轴交于点C
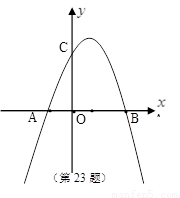
(1)求A、B、C三点的坐标?
(2)用配方法求该二次函数的对称轴和顶点坐标?
(3)若坐标平面内的点M,使得以点M和三点A、B、C为顶点的四边形是平行四边形,求点M的坐标?(直接写出M的坐标,不用说明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com