

���� ��1����������ó��ܵİ༶�����������Ͷ��ƪ��Ϊ2����Ӧ�����ε�Բ�ĽǵĶ�����
��2�����ü�Ȩƽ�����ó����ɣ�
��3��������״ͼ�ó����еĿ��ܽ����ó����ʣ�
��� 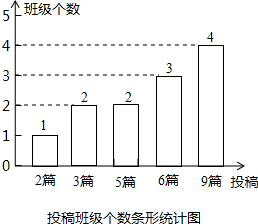 �⣺��1��3��25%=12��������$\frac{1}{12}$��360��=30�㣮
�⣺��1��3��25%=12��������$\frac{1}{12}$��360��=30�㣮
��Ͷ��ƪ��Ϊ2����Ӧ�����ε�Բ�ĽǵĶ���Ϊ30�㣮
��2��12-1-2-3-4=2��������
��2+3��2+5��2+6��3+9��4����12=72��12=6��ƪ����
��������ͳ��ͼ��������Ϊ��
��3������״ͼ���£� ��
��
�ܹ�12������������ͬһ�꼶����8�������
������ѡ�������ͬһ�꼶�ĸ���Ϊ��8��12=$\frac{2}{3}$��
���� ������Ҫ����������ͳ��ͼ�Լ�����ͳ��ͼ��Ӧ�ú���״ͼ������ʣ����������оٳ����еĿ����ǽ���ؼ���


 ������ҵ��ͬ����ϰ��ϵ�д�
������ҵ��ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
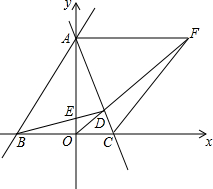 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��ֱ��AC�ֱ���x�ᣬy���ڵ�B��C��A������B��BD��AC��D����y�����E������BAC=45�㣬��B��C��E������ֱ�B��-3��0����C��2��0����E��0��1��������A��AF��x�ᣬ��OD���ӳ����ڵ�F������CF����ƽ��ֱ������ϵ�У��Ƿ���ڵ�K��ʹ��OKF���OCFȫ�ȣ������ڣ������K�����겢����ͼ�Σ��������ڣ�˵�����ɣ�
��ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��ֱ��AC�ֱ���x�ᣬy���ڵ�B��C��A������B��BD��AC��D����y�����E������BAC=45�㣬��B��C��E������ֱ�B��-3��0����C��2��0����E��0��1��������A��AF��x�ᣬ��OD���ӳ����ڵ�F������CF����ƽ��ֱ������ϵ�У��Ƿ���ڵ�K��ʹ��OKF���OCFȫ�ȣ������ڣ������K�����겢����ͼ�Σ��������ڣ�˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
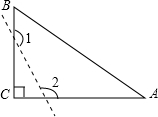 ��ͼ����֪��ABC�У���C=90�㣬����ͼ������ȥ��C�����1+��2���ڣ�������
��ͼ����֪��ABC�У���C=90�㣬����ͼ������ȥ��C�����1+��2���ڣ�������| A�� | 90�� | B�� | 135�� | C�� | 270�� | D�� | 315�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
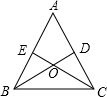 ��ͼ���ڡ�ABC�У���D��E�ֱ��ڱ�AC��AB�ϣ�BD��CE���ڵ�O�����������ĸ��������١�EBO=��DCO����BE=CD����OB=OC����OE=OD���������ĸ������У�ѡȡ���������������ж���ABC�ǵ��������ε��ǣ�������
��ͼ���ڡ�ABC�У���D��E�ֱ��ڱ�AC��AB�ϣ�BD��CE���ڵ�O�����������ĸ��������١�EBO=��DCO����BE=CD����OB=OC����OE=OD���������ĸ������У�ѡȡ���������������ж���ABC�ǵ��������ε��ǣ�������| A�� | �٢� | B�� | �٢� | C�� | �ۢ� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com