练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

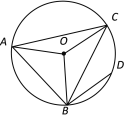
    【题目】如图，△ABC是⊙O的内接三角形，点D是弧BC的中点，已知∠AOB=98°，∠COB=120°．则∠ABD的度数是___．

    【答案】101°

    【解析】试题分析：根据周角为360°，可求出∠AOC的度数，由圆周角定理可求出∠ABC的度数，关键是求∠CBD的度数；由于D是弧BC的中点，根据圆周角定理知∠DBC=∠BAC，而∠BAC的度数可由同弧所对的圆心角∠BOC的度数求得，由此得解．

    解：∵∠AOB=98°，∠COB=120°，

    ∴∠AOC=360°-∠AOB-∠COB=142°；

    ∴∠ABC=71°；

    ∵D是的中点，

    ∴∠CBD=∠BAC；

    又∵∠BAC=∠COB=60°，

    ∴∠CBD=30°；

    ∴∠ABD=∠ABC+∠CBD=101°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】计算3a+2﹣4a﹣5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一只甲虫在5×5的方格(每个小格边长为1)上沿着网格线运动．它从A处出发去看望B，C，D处的其他甲虫．规定：向上、向右走为正，向下、向左走为负．如果从A到B记为：A→B(＋1，＋4)，从B到A记为：B→A(－1，－4)，其中第一个数表示左右方向，第二个数表示上下方向．

    (1)图中B→C(____，____)，C→____(＋1，____)；

    (2)若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】Rt△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点．令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．

    （1）若点P在线段AB上，如图（1）所示，且∠α=50°，则∠1+∠2= °；

    （2）若点P在边AB上运动，如图（2）所示，则∠α、∠1、∠2之间有何关系？说明理由．

    （3）若点P在Rt△ABC斜边BA的延长线上运动（CE＜CD），则∠α、∠1、∠2之间有何关系？猜想并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若三角形的两条边的长度是4cm和9cm，则第三条边的长度可能是（　　）

    A. 4 cmB. 5 cmC. 9 cmD. 13 cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】填写下列空格，完成证明．
    已知：如图，AD是△ABC的角平分线，点E在BC上，点F在CA的延长线上，EF∥AD，EF交AB于点G．
    求证：∠3=∠F
    证明：因为AD是△ABC的角平分线 （ 已知 ）
    所以∠1=∠2 （）
    因为EF∥AD（已知）
    所以∠3=∠（）
    ∠F=∠（）
    所以∠3=∠F（）．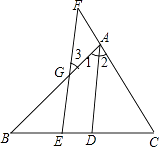

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】王老师对本班40名学生的血型作了统计，列出如下的统计表，则本班A型血的人数是( )

    组别

    A型

    B型

    AB型

    O型

    频率

    0.4

    0.35

    0.1

    0.15

    A. 16人 B. 14人 C. 4人 D. 6人

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把角度21.3°化成度、分、秒的形式： ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，禁止捕鱼期间，某海上稽查队在某海域巡逻，上午某一时刻在A处接到指挥部通知，在他们东北方向距离12海里的B处有一艘捕鱼船，正在沿南偏东75°方向以每小时10海里的速度航行，稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发，在C处成功拦截捕鱼船，求巡逻船从出发到成功拦截捕鱼船所用的时间.

    查看答案和解析>>

    同步练习册答案