
【题目】如图,∠AOB=110°,OD平分∠BOC,OE平分∠AOC. 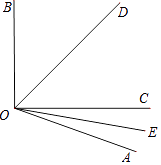
(1)求∠EOD的度数.
(2)若∠BOC=90°,求∠AOE的度数.
【答案】
(1)解:∵OD平分∠BOC,OE平分∠AOC,
∴∠COD= ![]() ∠BOC,∠COE=
∠BOC,∠COE= ![]() ∠AOC,
∠AOC,
∴∠EOD=∠COD+∠COE
= ![]() (∠BOC+∠AOC)
(∠BOC+∠AOC)
= ![]() ∠AOB
∠AOB
=55°
(2)解:由于∠AOC=∠AOB﹣∠BOC=110°﹣90°=20°,
∵OE平分∠AOC,
∴∠AOE= ![]() ∠AOC=10°
∠AOC=10°
【解析】(1)由OD平分∠BOC,OE平分∠AOC,可知∴∠EOD=∠COD+∠COE= ![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)= ![]() ∠AOB=55°;
∠AOB=55°;
【考点精析】利用角的平分线和角的运算对题目进行判断即可得到答案,需要熟知从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示.


科目:初中数学 来源: 题型:
【题目】某公司为了评价甲、乙两位营销员去年的营销业绩,统计了这两人去年12个月的营销业绩(所推销商品的件数)分别如下图所示:
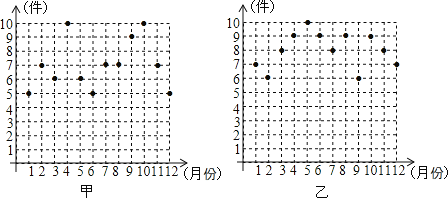
(1)利用图中信息,完成下表:
平均数 | 中位数 | 众数 | 方差 | |
甲 | 7 | |||
乙 | 1.5 |
(2)假若你是公司主管,请你根据(1)中图表信息,应用所学的统计知识,对两人的营销业绩作出评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红把一枚硬币抛掷10次,结果有4次正面朝上,那么( )
A. 正面朝上的频数是0.4 B. 反面朝上的频数是6
C. 正面朝上的频率是4 D. 反面朝上的频率是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某制衣厂某车间计划用10天加工一批出口童装和成人装共360件,该车间的加工能力是:每天能单独加工童装45件或成人装30件.
(1)该车间应安排几天加工童装,几天加工成人装,才能如期完成任务?(列方程组解答)
(2)若加工童装一件可获利25元,加工成人装一件可获利50元,那么该车间加工完这批服装后,共可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面关于平行四边形的说法中错误的是( )
A. 平行四边形的两条对角线相等
B. 平行四边形的两条对角线互相平分
C. 平行四边形的对角相等
D. 平行四边形的对边相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0),交y轴于点C,点D是线段OB上一动点,连接CD,将CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF,CE交于点G.
(1)求抛物线解析式;
(2)求线段DF的长;
(3)当DG=![]() 时,
时,
①求tan∠CGD的值;
②试探究在x轴上方的抛物线上,是否存在点P,使∠EDP=45°?若存在,请写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com