
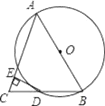
【题目】如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.
科目:初中数学 来源: 题型:
【题目】圆柱底面周长为4cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在直线l外,点B在直线l上.
(1)在l上求作一点C,在l外求作一点D,使得以A、B、C、D为顶点的四边形是菱形;(要求:用直尺和圆规作出所有大小不同的菱形)
(2)连接AB,若AB=5,且点A到直线l的距离为4,通过计算,找出(1)中面积最小的菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2( ),
且∠1=∠4( )
∴∠2=∠4(等量代换)
∴CE∥BF( )
∴∠ =∠3( )
又∵∠B=∠C(已知)
∴∠3=∠B( )
∴AB∥CD( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,错误的选法是( )
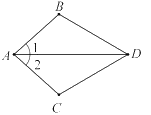
A. ∠ADB=∠ADCB. ∠B=∠CC. DB=DCD. AB=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折叠矩形纸片:
第一步,如图1,在纸片一端折出一个正方形MBCN,再把纸片展开;
第二步,如图2,把这个正方形对折,再把纸片展开,得矩形MAEN和ABCE;
第三步,如图3,折出矩形ABCE的对角线EB,并把EB折到图中所示的ED处;
第四步,如图4,展平纸片,按所得点D折出DF,得矩形BFDC.
(1)若MN=2时,CM=________;
(2)![]() 的值为 ________.
的值为 ________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
(1)求证:△ADE≌△ABF;
(2)若BC=8,DE=6,求△AEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了加强训练学生的篮球和足球运球技能,准备购买一批篮球和足球用于训练,已知1个篮球和2个足球共需116元;2个篮球和3个足球共需204元
![]() 求购买1个篮球和1个足球各需多少元?
求购买1个篮球和1个足球各需多少元?
![]() 若学校准备购进篮球和足球共40个,并且总费用不超过1800元,则篮球最多可购买多少个?
若学校准备购进篮球和足球共40个,并且总费用不超过1800元,则篮球最多可购买多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com