
【题目】数学课上,李老师出示了如下框中的题目.
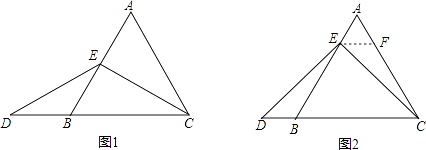
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AEDB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AEDB(填“>”,“<”或“=”).理由如下:
如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
【答案】
(1)=
(2)=
(3)
解:分为四种情况:
如图1:
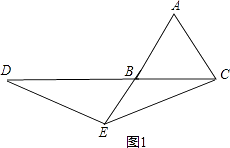
∵AB=AC=1,AE=2,
∴B是AE的中点,
∵△ABC是等边三角形,
∴AB=AC=BC=1,△ACE是直角三角形(根据直角三角形斜边的中线等于斜边的一半),
∴∠ACE=90°,∠AEC=30°,
∴∠D=∠ECB=∠BEC=30°,∠DBE=∠ABC=60°,
∴∠DEB=180°﹣30°﹣60°=90°,
即△DEB是直角三角形.
∴BD=2BE=2(30°所对的直角边等于斜边的一半),
即CD=1+2=3.
如图2,
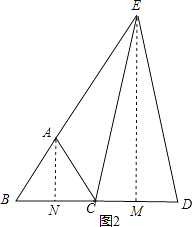
过A作AN⊥BC于N,过E作EM⊥CD于M,
∵等边三角形ABC,EC=ED,
∴BN=CN= ![]() BC=
BC= ![]() ,CM=MD=
,CM=MD= ![]() CD,AN∥EM,
CD,AN∥EM,
∴△BAN∽△BEM,
∴ ![]() ,
,
∵△ABC边长是1,AE=2,
∴ ![]() =
= ![]() ,
,
∴MN=1,
∴CM=MN﹣CN=1﹣ ![]() =
= ![]() ,
,
∴CD=2CM=1;
如图3,
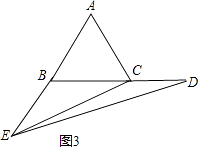
∵∠ECD>∠EBC(∠EBC=120°),而∠ECD不能大于120°,否则△EDC不符合三角形内角和定理,
∴此时不存在EC=ED;
如图4
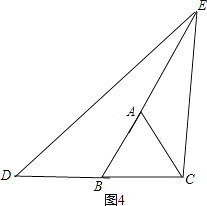
∵∠EDC<∠ABC,∠ECB>∠ACB,
又∵∠ABC=∠ACB=60°,
∴∠ECD>∠EDC,
即此时ED≠EC,
∴此时情况不存在,
答:CD的长是3或1.
【解析】解:(1.)答案为:=.
(2.)答案为:=.
证明:在等边△ABC中,∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∴∠AEF=∠AFE=∠BAC=60°,
∴AE=AF=EF,
∴AB﹣AE=AC﹣AF,
即BE=CF,
∵∠ABC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∵ED=EC,
∴∠EDB=∠ECB,
∵∠EBC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∴∠BED=∠FCE,
在△DBE和△EFC中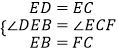 ,
,
∴△DBE≌△EFC(SAS),
∴DB=EF,
∴AE=BD.
(1)根据等边三角形的性质和三角形的内角和定理求出∠D=∠ECB=30°,∠ABC=60°,求出∠D=∠DEB=30°,推出DB=BE=AE即可得到答案;(2)作EF∥BC,证出等边三角形AEF,再证△DBE≌△EFC即可得到答案;(3)分为四种情况:画出图形,根据等边三角形性质求出符合条件的CD即可.


科目:初中数学 来源: 题型:
【题目】如图是某居民小区的一块宽为2a米,长为b米的长方形空地,为了美化环境,准备在这块长方形空地的四个顶点处修建一个半径为a米的扇形花台,然后在花台内种花,其余种草.
(1)请分别用含a、b的式子表示种花和种草的面积.(答案保留π)
(2)如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?(答案保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
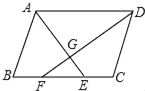
【题目】如图,在ABCD中,∠BAD、∠ADC的平分线AE、DF分别交BC于点E、F,AE与DF相交于点G.
(1)求证:∠AGD=90°.
(2)若CD=4cm,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣ ![]() (x﹣1)2+3与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
(x﹣1)2+3与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.
(1)如图1.求点A的坐标及线段OC的长;
(2)点P在抛物线上,直线PQ∥BC交x轴于点Q,连接BQ.
①若含45°角的直角三角板如图2所示放置.其中,一个顶点与点C重合,直角顶点D在BQ上,另一个顶点E在PQ上.求直线BQ的函数解析式;
②若含30°角的直角三角板一个顶点与点C重合,直角顶点D在直线BQ上,另一个顶点E在PQ上,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.

(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.
(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,BD是一条对角线,点P在CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QM⊥BD于M,连接AM,PM(如图1).

(1)判断AM与PM的数量关系与位置关系并加以证明;
(2)若点P在线段CD的延长线上,其它条件不变(如图2),(1)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m cm,宽为n cm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )cm.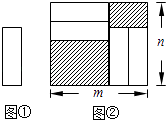
A.4m
B.4n
C.2(m+n)
D.4(m﹣n)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com