
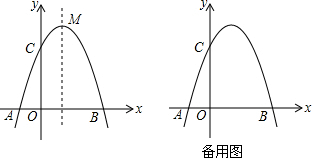
���� ��1�����B���C�����꣬���ý���ʽ�����������ʽ��
��2���ٹʿ���ֱ��l�ı���ʽΪy=kx+3������GFΪRt��AEN��λ�ߣ�FΪEN�е㣬�õ�G��0��$\frac{k+3}{2}$����F��1��$\frac{k+3}{2}$�������GF��AE��֤����AOG�ס�CNG��
�ڽ�ֱ��l����ƽ�ƣ���ƽ�ƺ��ֱ��Ϊl�䣬��ֱ��l����������ֻ��һ������Q1ʱ����Q1���߶�CD���ɡ�Q1CD���߶�CD�·���һ����Q2���ɡ�Q2CD����ʱ���������ĵ�Q����ֻ�����������ֱ��l��ı���ʽΪy=-$\frac{3}{4}$x+$\frac{313}{64}$������ı���CP1Q1C����ƽ���ı��Σ��õ�P1Q1=CC��=$\frac{313}{64}$-3=$\frac{121}{64}$����S=S��Q1CP1+S��Q1DP1�ɵõ�S=$\frac{1331}{512}$ʱ����Ӧ�ĵ�Q����ֻ��������
��� �⣺��1����y=ax2-2ax+c=a��x-1��2+c-a2��
�������ߵĶԳ���Ϊֱ��x=1��
��������y=ax2-2ax+c��x�ύ��A��B����A������Ϊ��-1��0����
���B��������3��0����OB=3��
�ɵø������ߵı���ʽΪy=a��x+1����x-3����
��OB=OC����������y��������ύ�ڵ�C��
��OC=3����C��������0��3����
����C���������ñ���ʽ�����a=-1��
��������ߵı���ʽΪy=-x2+2x+3��
��y=-��x-1��2+4��
�ඥ��M������Ϊ��1��4����
��2���������߶���M��ME��x�ᣬ����ΪE����ME�ı���ʽΪx=1���������߶Գ��ᣮ
����ͼ1��ֱ��l�������߶Գ���ME���ڵ�N������AN��y���ڵ�G����G��GF��ME�ڵ�F
��ֱ��l������C��0��3�����ʿ���ֱ��l�ı���ʽΪy=kx+3��
���N������1��k+3����
��Rt��AEN�У�OΪAE�е㣬OG��EN��
��OGΪRt��AEN��λ�ߣ�GΪAN�е㣬
�֡�GF��ME��
��GF��AE��
��GFΪRt��AEN��λ�ߣ�FΪEN�е㣬
��G��0��$\frac{k+3}{2}$����F��1��$\frac{k+3}{2}$����
��GF=1��NF=EF=OG=$\frac{k+3}{2}$��CG=3-$\frac{k+3}{2}$=$\frac{3-k}{2}$��
�֡�AN��l��
���AOG�ס�CNG��
��$\frac{CG}{AG}$=$\frac{NG}{OG}$����$\frac{\frac{3-k}{2}}{\sqrt{{1}^{2}+��\frac{k+3}{2}��^{2}}}$=$\frac{\sqrt{{1}^{2}+��\frac{k+3}{2}��^{2}}}{\frac{k+3}{2}}$��
�����ã�k2+3k+2=0��
��k=-1��k=-2��
�൱AN��lʱ��ֱ��l�ĺ�������ʽΪy=-x+3��y=-2x+3��
�ڽ�ֱ��l����ƽ�ƣ���ƽ�ƺ��ֱ��Ϊl�䣬��ֱ��l����������ֻ��һ������Q1ʱ����Q1���߶�CD���ɡ�Q1CD���߶�CD�·���һ����Q2���ɡ�Q2CD����ʱ���������ĵ�Q����ֻ��������
��ֱ��l��ı���ʽΪy=-$\frac{3}{4}$x+b�����������ߵı���ʽ�ã�
-x2+2x+3=-$\frac{3}{4}$x+b�������ã�4x2-11x+4b-12=0��
��l����������ֻ��һ������ʱ����=��-11��2-4��4����4b-12��=0�����b=$\frac{313}{64}$��
��ֱ��l��ı���ʽΪy=-$\frac{3}{4}$x+$\frac{313}{64}$��
��֪�ı���CP1Q1C����ƽ���ı��Σ�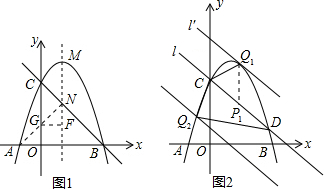
��P1Q1=CC��=$\frac{313}{64}$-3=$\frac{121}{64}$��
��-x2+2x+3=-$\frac{3}{4}$x+3����x=0����ȥ����x=$\frac{11}{4}$��
���D�ĺ�����Ϊ$\frac{11}{4}$��
��S=S��Q1CP1+S��Q1DP1=$\frac{1}{2}$��$\frac{121}{64}$��$\frac{11}{4}$=$\frac{1331}{512}$��
�ʵ�S=$\frac{1331}{512}$ʱ����Ӧ�ĵ�Q����ֻ��������
���� ���⿼���˶��κ����ۺ��⣬��1���漰����ϵ��������κ�������ʽ��Ҫ��Ϥ����ʽ����2�����漰����ϵ������һ�κ�������ʽ�������ε���λ�߶�����֪ʶ�����Ǵ��������⣬Ҫ���ͼ���ҵ����ڵĵ㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
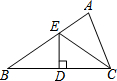 ��ͼ���ڡ�ABC�У�BC�ߵĴ�ֱƽ����DE����BC�ڵ�D������AB�ڵ�E������EDC���ܳ�Ϊ24����ABC���ı���AEDC���ܳ�֮��Ϊ12�����߶�DE�ij�Ϊ��������
��ͼ���ڡ�ABC�У�BC�ߵĴ�ֱƽ����DE����BC�ڵ�D������AB�ڵ�E������EDC���ܳ�Ϊ24����ABC���ı���AEDC���ܳ�֮��Ϊ12�����߶�DE�ij�Ϊ��������| A�� | 18 | B�� | 12 | C�� | 6 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
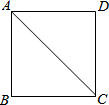 ��ͼ��������ABCD�ı߳�Ϊ2����a��AC��b������a��bΪ������������������ab��ֵΪ��������
��ͼ��������ABCD�ı߳�Ϊ2����a��AC��b������a��bΪ������������������ab��ֵΪ��������| A�� | 2 | B�� | 5 | C�� | 6 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{2}{3}$ | B�� | $\frac{2}{3}$ | C�� | -$\frac{3}{2}$ | D�� | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
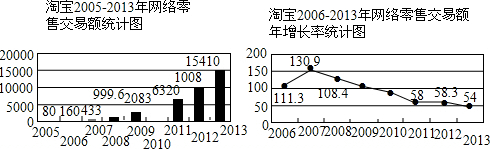
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 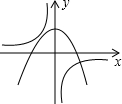 | B�� | 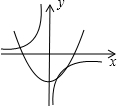 | C�� | 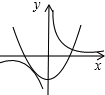 | D�� | 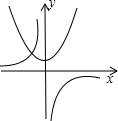 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com