
分析 (1)根据定义即可求出-x2+2x-3的“牛郎织女式”;
(2)根据定义求出m与n的值,代入原式求值即可;
(3)利用作差法即可求出a的范围.
解答 解:(1)设-x2+2x-3的“牛郎织女式”为ax2+bx+c
由题意可知:a=1,b=-2,c=3,
∴-x2+2x-3的“牛郎织女式”为x2-2x+3;
(2)由题意可知:-18m-2n=0,-3+n=0,
解得:m=-$\frac{1}{3}$,n=3,
∴原式=(-1)2015=-1;
(3)x2-2x+a的“牛郎织女式”为-x2+2x-a,
∴由题意可知:x2-2x+a>-x2+2x-a对于任何x都成立,
∴x2-2x+a-(-x2+2x-a)>0,
∴a>-x2+2x,
∴a>-(x-1)2+1对于任何的x都成立,
∵-(x-1)2+1的最大值为1,
∴a>1,
点评 本题考查学生的阅读理解能力,涉及相反数的性质,解方程,代入求值,不等式的解法,配方法求值最值等知识.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:解答题
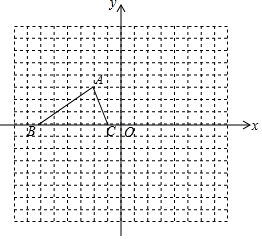 如图,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1组 | B. | 3组 | C. | 4组 | D. | 7组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
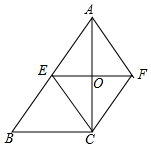 如图,在四边形ABCF中,∠ACB=90°,点E是AB边的中点,点F恰是点E关于AC所在直线的对称点.
如图,在四边形ABCF中,∠ACB=90°,点E是AB边的中点,点F恰是点E关于AC所在直线的对称点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
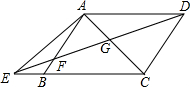 如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且$\frac{FG}{GD}$=$\frac{AD}{CE}$.
如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且$\frac{FG}{GD}$=$\frac{AD}{CE}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com