
分析 (1)根据方程的系数结合根的判别式,即可得出△=(2k-1)2+3>0,从而可得出不论k取何值时,方程x2-2kx+k-1=0总有两个不相等的实数根,即不论k取何值时,抛物线与x轴必有两个交点;
(2)由根与系数的关系可得出x1+x2=2k、x1•x2=k-1,将其代入x12+x22=(x1+x2)2-2x1•x2中,再利用配方法即可找出x12+x22的最小值.
解答 (1)证明:∵在关于x的一元二次方程x2-2kx+k-1=0中,△=(-2k)2-4(k-1)=(2k-1)2+3>0,
∴不论k取何值时,方程x2-2kx+k-1=0总有两个不相等的实数根,
∴不论k取何值时,抛物线与x轴必有两个交点.
(2)解:∵抛物线与x轴的两个交点分别为(x1,0)、(x2,0),
∴x1+x2=2k,x1•x2=k-1,
∴x12+x22=(x1+x2)2-2x1•x2=4k2-2k+2=4(k-$\frac{1}{4}$)2+$\frac{7}{4}$,
∴当k=$\frac{1}{4}$时,x12+x22取最小值,最小值为$\frac{7}{4}$.
点评 本题考查了抛物线与x轴的交点、二次函数的性质、二次函数的最值、根的判别式以及根与系数的关系,解题的关键是:(1)找出不论k取何值时,方程x2-2kx+k-1=0总有两个不相等的实数根;(2)利用配方法找出x12+x22的最小值.


科目:初中数学 来源: 题型:选择题

| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2017}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
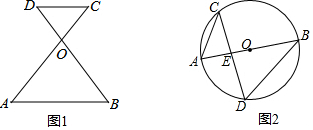
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
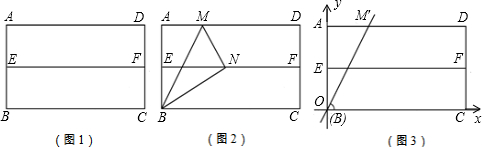
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
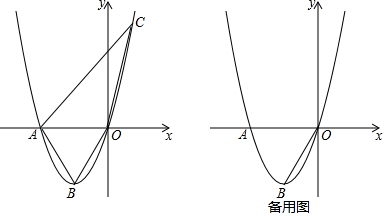
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
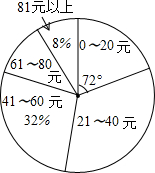 某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:
某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:| 捐款 | 人数 |
| 0~20元 | |
| 21~40元 | |
| 41~60元 | |
| 61~80元 | 6 |
| 81元以上 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (120-30$\sqrt{5}$)cm | B. | (160-60$\sqrt{5}$)cm | C. | (60$\sqrt{5}$-120)cm | D. | (60$\sqrt{5}$-6)cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com