
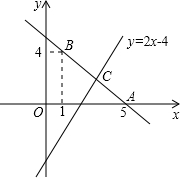
 已知直线y=kx+b经过点A(5,0),B(1,4).
已知直线y=kx+b经过点A(5,0),B(1,4).分析 (1)利用待定系数法即可求得函数的解析式;
(2)关于x的不等式2x-4≤kx+b的解集就是函数y=2x-4落在y=kx+b的图象下方的部分对应的自变量的取值范围.
解答 解:(1)根据题意得$\left\{\begin{array}{l}{5k+b=0}\\{k+b=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$,
则直线AB的解析式是y=-x+5;
(2)根据图象可得不等式的解集是x≤3.
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.也考查了待定系数法求直线的解析式.


科目:初中数学 来源: 题型:选择题
| A. | m>5 | B. | m<-5 | C. | m≥5 | D. | m≥-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
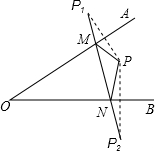 如图,∠AOB=30°,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,OP=18,图中线段之间相等的关系式有(至少写出两组)PM=P1M,PN=P2N;△PMN的周长为18.
如图,∠AOB=30°,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,OP=18,图中线段之间相等的关系式有(至少写出两组)PM=P1M,PN=P2N;△PMN的周长为18.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
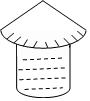 如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元,那么购买油毡所需要的费用是565.2元(结果保留一位小数).
如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元,那么购买油毡所需要的费用是565.2元(结果保留一位小数).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直线外一点到这条直线的垂线段,叫做点到直线的距离 | |
| B. | 两条直线被第三条直线所截,内错角相等 | |
| C. | 若两条直线相交所成的四个角相等,则这两条直线互相垂直 | |
| D. | 相等的两个角是对顶角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
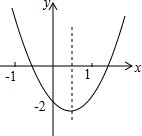 二次函数y=ax2+bx+c的图象如图所示,则下列结论:①abc<0;②b2-4ac>0;③2a+b>0;④a+b+c<0;⑤ax2+bx+c+2=0的解为x=0,其中正确的有( )
二次函数y=ax2+bx+c的图象如图所示,则下列结论:①abc<0;②b2-4ac>0;③2a+b>0;④a+b+c<0;⑤ax2+bx+c+2=0的解为x=0,其中正确的有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
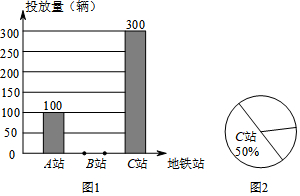
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com