
 由示意图可见,抛物线y=x2+px+q若有两点A(a,yl)、B(b,y2)(其中a<b)在x轴下方,则抛物线必与x轴有两个交点C(x1,O)、D(x2,O)(其中xl<x2),且满足xl<a<b<x2.当A(1,-2005),且xl、x2均为整数时,求二次函数的表达式.
由示意图可见,抛物线y=x2+px+q若有两点A(a,yl)、B(b,y2)(其中a<b)在x轴下方,则抛物线必与x轴有两个交点C(x1,O)、D(x2,O)(其中xl<x2),且满足xl<a<b<x2.当A(1,-2005),且xl、x2均为整数时,求二次函数的表达式. 分析 因为抛物线与x轴有两个交点C(x1,O)、D(x2,O)(其中xl<x2),所以可设抛物线解析式为y=(x-x1)(x-x2),再把A点(1,-2005)代入函数的解析式可整理得:-2005=(1-x1)(1-x2),又因为xl、x2均为整数,所以可求出满足题意的xl、x2的值,进而可求出二次函数的表达式.
解答 解:
∵抛物线与x轴有两个交点C(x1,O)、D(x2,O)(其中xl<x2),
∴可设抛物线解析式为y=(x-x1)(x-x2),
把A(1,-2005)代入y=(x-x1)(x-x2),得-2005=(1-x1)(1-x2).
由xl、x2为整数,且2005=5×401得$\left\{{\begin{array}{l}{1-{x_1}=-2005}\\{1-{x_2}=1}\end{array}}\right.$;$\left\{{\begin{array}{l}{1-{x_1}=1}\\{1-{x_2}=-2005}\end{array}}\right.$;$\left\{{\begin{array}{l}{1-{x_1}=401}\\{1-{x_2}=-5}\end{array}}\right.$;$\left\{{\begin{array}{l}{1-{x_1}=5}\\{1-{x_2}=-401}\end{array}}\right.$
分别解得:x1=-2004,x2=2,则y=x2+2002x-4008;x1=0,x2=2006,则y=x2+2006x;
x1=-400,x2=6,则y=x2+394x-2004;x1=-4,x2=402,则y=x2+398x-1608.
经检验,所求的抛物线有以下4条:
y=x2+2002x-4008;y=x2+2006x;y=x2+394x-2004;y=x2+398x-1608.
点评 本题考查了二次函数综合性题目,熟知二次函数的三种表达形式分别是:一般式、交点式、顶点式是解题的关键,


科目:初中数学 来源: 题型:填空题
 如图,⊙O的直径AB=2,P是上半圆(A、B除外)上任一点,∠APB的平分线交⊙O于C,弦EF过AC、BC的中点M、N,则EF的长是$\sqrt{3}$.
如图,⊙O的直径AB=2,P是上半圆(A、B除外)上任一点,∠APB的平分线交⊙O于C,弦EF过AC、BC的中点M、N,则EF的长是$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,AB=a,BC=b,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,且y关于x的函数图象大致如图:
如图,矩形ABCD中,AB=a,BC=b,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,且y关于x的函数图象大致如图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
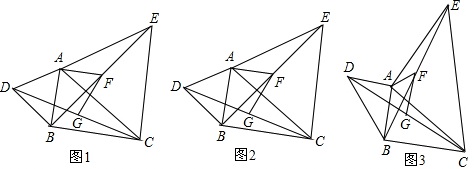
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
如图,抛物线y=-x2+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小杰同学研究两平行线被第三条直线所截构成的同位角、内错角、同旁内角的角平分线的位置关系发现了一些比较特殊,你也有同样的发现吗?
小杰同学研究两平行线被第三条直线所截构成的同位角、内错角、同旁内角的角平分线的位置关系发现了一些比较特殊,你也有同样的发现吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com