
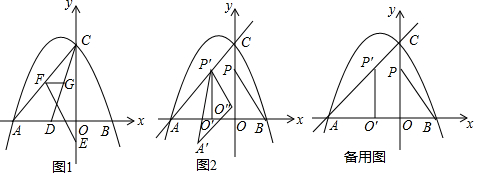
分析 (1)先求得点A和点C的坐标,然后利用待定系数法求得直线AC的解析式即可;
(2)先求得CD的解析式,设点F的坐标为(a,$\frac{3}{4}$a+3),点G的坐标为(x,2x+3).然后依据点F和点G的坐标相等可求得点G的横坐标(用含a的式子表示),从而可求得FG的上,然后列出△FGE的面积与a的函数关系,利用二次函数的性质可求得a的值,从而得到点F的坐标,作点N关于y轴的对称点N′,在x轴上取点E使NN′=BE=2,则E(4,0).然后证明MN=MN′、BN=N′E,由两点之间线段最短可知:当点F、M、N′、E在一条直线上时,FM+MN+NB有最小值,最后依据勾股定理求的FE的值即可;
(3)如图2所示:当AI=AH时,作AM平分∠CAO,交AC于点M,作MN⊥AC,垂足为N.先利用面积法求得OM的值,然后可求得tan∠MOA的值,然后在Rt△IP′O″中,利用锐角三角函数的定义可求得IP′的值,最后依据AI=IP′-AP′求解即可;如图3所示:当AH=IH时.可证明△IP′A′为等腰三角形即IP′=P′A′;如图4所示:当AI=AH时,过点A作AM⊥IH,可证明∠IP′O″=∠IAM,然后在Rt△IO″P′利用锐角三角函数的定义可求得IP′的长,最后依据AI=IP′+AP′求解即可;如图5所示:当IA=IH时.作IM⊥P′A′.可证明△IP′A′为等腰直角三角形,然后再Rt△IMP′可利用锐角三角函数的定义求得IP′的长.,最后依据AI=IP′+AP′求解即可.
解答 解:(1)把x=0代入得:y=3,
∴C(0,3).
把y=0代入得:0=-$\frac{3}{8}$x2$-\frac{3}{4}$x+3,解得x=2或x=-4.
∴A(-4,0)、B(2,0).
设直线AC的解析式为y=kx+b,将C(0,3)、A(-4,0)代入得:$\left\{\begin{array}{l}{b=3}\\{-4k+b=0}\end{array}\right.$,
解得k=$\frac{3}{4}$,b=3.
∴直线AC的解析式为y=$\frac{3}{4}$x+3.
(2)∵OD=$\frac{3}{2}$,
∴D(-$\frac{3}{2}$,0).
设CD的解析式为y=mx+n,将点C、D的坐标代入得:$\left\{\begin{array}{l}{n=3}\\{-\frac{3}{2}m+n=0}\end{array}\right.$,解得n=3,m=2,
∴直线CD的解析式为y=2x+3.
设点F的坐标为(a,$\frac{3}{4}$a+3),点G的坐标为(x,2x+3).
∵FG∥x轴,
∴$\frac{3}{4}$a+3=2x+3,解得:x=$\frac{3}{8}$a.
∴FG=-$\frac{5}{8}$a.
∴△FGE的面积=$\frac{1}{2}$FG•|Gy-Ey|=$\frac{1}{2}$×(-$\frac{5}{8}$a)×($\frac{3}{4}$a+4)=-$\frac{15}{64}$a2-$\frac{5}{4}$a.
∴当a=-$\frac{8}{3}$时,△FGE的面积有最大值.
∴F(-$\frac{8}{3}$,1).
如图1所示:作点N关于y轴的对称点N′,在x轴上取点E使NN′=BE=2,则E(4,0).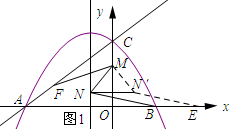
∵N与N′关于y轴对称,
∴MN=MN′.
∵NN′∥BE且NN′=BE,
∴四边形NN′EB为平行四边形.
∴BN=N′E.
∴FM+MN+NB=AM+MN′+N′E.
由两点之间线段最短可知:当点F、M、N′、E在一条直线上时,FM+MN+NB有最小值,
∴FM+MN+NB=EF=$\sqrt{(4+\frac{8}{3})^{2}+{1}^{2}}$=$\frac{\sqrt{409}}{3}$.
由两点之间线段最短可知:当点F、M、N′、E在一条直线上时,FM+MN+NB有最小值,
∴FM+MN+NB=EF=$\sqrt{(4+\frac{8}{3})^{2}+{1}^{2}}$=$\frac{\sqrt{409}}{3}$.
(3)如图2所示:当AI=AH时,作AM平分∠CAO,交AC于点M,作MN⊥AC,垂足为N.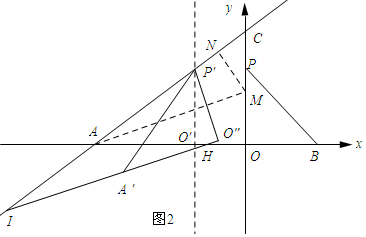
∵直线AC的解析式为y=$\frac{3}{4}$x+3,
∵AM平分∠CAO,MO⊥AO,MN⊥AC,
∴MN=MO.
∵AO=4,OC=3,
∴AC=5.
设MN=MO=a.
∵△AOC的面积=$\frac{1}{2}$AC•MN+$\frac{1}{2}$AO•OM=$\frac{1}{2}$AO•OC,
∴$\frac{1}{2}$×5×a+$\frac{1}{2}$×4×a=$\frac{1}{2}$×3×4,解得:a=$\frac{4}{3}$.
∴MO=$\frac{4}{3}$.
∴tan∠MAO=$\frac{\frac{4}{3}}{4}$=$\frac{1}{3}$.
∵AI=AH,
∴∠AIH=∠AHI.
又∵∠AIH+∠AHI=∠CAO,AM平分∠CAO,
∴tan∠AIO″=tan∠MAO.
∴tan∠AIO″=tan∠MAO=$\frac{1}{3}$.
∵P′O″=P′O′=OP=PB=2,
∴IO″=6.
依据勾股定理可知IP′=2$\sqrt{10}$.
∵$\frac{P′O′}{AP′}$=$\frac{3}{5}$,
∴AP′=$\frac{10}{3}$.
∴AI=IP′-AP′=2$\sqrt{10}$-$\frac{10}{3}$.
如图3所示:当AH=IH时.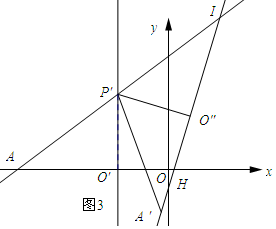
∵AH=IH,
∴∠IAH=∠AIH.
由旋转的性质可知∠IAH=∠P′A′I.
∴∠P′A′I=∠P′IA′.
∴P′I=P′A′.
∴P′I=AP′=$\frac{10}{3}$.
∴AI=$\frac{20}{3}$.
如图4所示:当AI=AH时,过点A作AM⊥IH.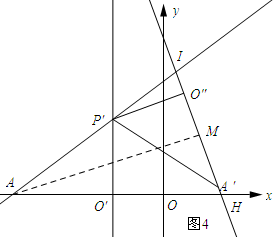
∵P′O″⊥IH,AM⊥IH,
∴O″P′∥AM.
∴∠IAM=∠IP′O″.
∵AI=AH,AM⊥IH,
∴∠IAM=∠IP′O″.
∴$\frac{IO″}{P′O″}$=$\frac{1}{3}$,$\frac{IO″}{2}=\frac{1}{3}$,解得:IO″=$\frac{2}{3}$.
依据勾股定理得:IP′=$\sqrt{{2}^{2}+(\frac{2}{3})^{2}}$=$\frac{2\sqrt{10}}{3}$.
∴AI=AP′+IP′=$\frac{10+2\sqrt{10}}{3}$.
如图5所示:当IA=IH时.作IM⊥P′A′.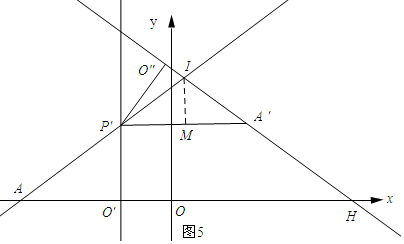
∵AI=IH,
∴∠IAH=∠IHA.
∵IA′P′=P′AO′,
∴∠IA′M=∠IHA.
∴P′A′∥AH.
∴△IP′A′为等腰三角形.
又∵IM⊥P′A′,
∴P′M=MA′=$\frac{5}{3}$.
∴IP′=$\frac{25}{12}$.
∴AI=$\frac{10}{3}$+$\frac{25}{12}$=$\frac{65}{12}$.
综上所述,当△AHI为等腰三角形时,AI的长为2$\sqrt{10}$-$\frac{10}{3}$或$\frac{20}{3}$或$\frac{10+2\sqrt{10}}{3}$或$\frac{65}{12}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求函数的解析式、二次函数的性质、轴对称图形的性质、平行四边形的性质、等腰三角形的性质、锐角三角函数的定义,将FM+MN+NB转化为EF的长是解答问题(2)的关键,根据题意画出图形是解答问题(3)的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 遗爱湖公园的亲水平台修建了许多台阶(如图所示),春季湖水上涨后有一部分在水下.如果点C的坐标为(-1,1),D点的坐标为(0,2).(点C、D分别在第3、4级)
遗爱湖公园的亲水平台修建了许多台阶(如图所示),春季湖水上涨后有一部分在水下.如果点C的坐标为(-1,1),D点的坐标为(0,2).(点C、D分别在第3、4级)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
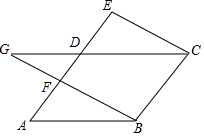 如图,在?ABCD中,AD=4,AB=5,延长AD到点E,连接EC过点B作BF∥CE交AD于点F,交CD的延长线于点G.
如图,在?ABCD中,AD=4,AB=5,延长AD到点E,连接EC过点B作BF∥CE交AD于点F,交CD的延长线于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
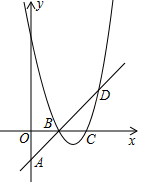 已知抛物线y=ax2+bx+8(a≥1)过点D(5,3),与x轴交于点B、C(点B、C均在y轴右侧)且BC=2,直线BD交y轴于点A.
已知抛物线y=ax2+bx+8(a≥1)过点D(5,3),与x轴交于点B、C(点B、C均在y轴右侧)且BC=2,直线BD交y轴于点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
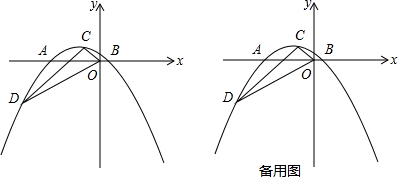
 如图,在Rt△ABC中,∠BAC=90°,AB>AC,射线AM平分∠BAC.
如图,在Rt△ABC中,∠BAC=90°,AB>AC,射线AM平分∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9 | B. | -9 | C. | 1 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com