
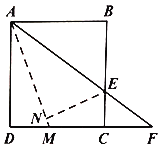
【题目】如图,正方形![]() 的边长为6,点
的边长为6,点![]() 是
是![]() 上的一点,连接
上的一点,连接![]() 并延长交射线
并延长交射线![]() 于点
于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,
处,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,当
,当![]() 时,则
时,则![]() 的长为________.
的长为________.
【答案】![]()
【解析】
根据翻折变换的性质可得AN=AB,∠BAE=∠NAE,再根据两直线平行,内错角相等可得∠BAE=∠F,从而得到∠NAE=∠F,根据等角对等边可得AM=FM,设CM=x,表示出DM、AM,然后利用勾股定理列方程求出x的值,从而得到AM的值,最后根据NM=AM-AN计算即可得解.
∵△ABE沿直线AE翻折,点B落在点N处,
∴AN=AB=6,∠BAE=∠NAE,
∵正方形对边AB∥CD,
∴∠BAE=∠F,
∴∠NAE=∠F,
∴AM=FM,
设CM=x,∵AB=2CF=8,
∴CF=3
∴DM=6x,AM=FM=3+x,
在Rt△ADM中,由勾股定理得,![]() ,
,
即![]()
解得x=![]() ,
,
所以,AM=3+![]() =
=![]() ,
,
所以,NM=AMAN=![]() 6=
6=![]()


科目:初中数学 来源: 题型:
【题目】某学校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目供学生选择,为了估计全校学生对这四个活动项日的选择情况,体育老师从全体学生中随机抽取了部分学生进行调查(规定每人必须并且只能选择其中的一个项目),并把调查结果绘制成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
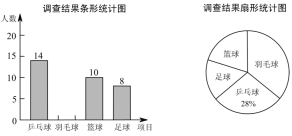
(1)求参加这次调查的学生人数,并补全条形统计图;
(2)求扇形统计图中“篮球”项目所对应扇形的圆心角度数;
(3)若该校共有1600名学生,试估计该校选择“足球”项目的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
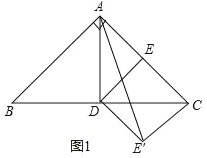
【题目】在等腰直角三角形ABC中,∠BAC=90°,AB=AC,D是斜边BC的中点,连接AD.
(1)如图1,E是AC的中点,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′,当AD=![]() 时,求AE的值.
时,求AE的值.
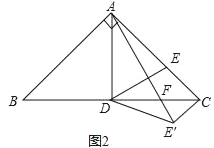
(2)如图2,在AC上取一点E,使得CE=![]() AC,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′交BC于点F,求证:DF=CF.
AC,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′交BC于点F,求证:DF=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合),通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于点E,延长EG 交CD于点F.如图①,当点H与点C重合时,易证得FG=FD(不要求证明);如图②,当点H为边CD上任意一点时,求证:FG=FD.
【应用】在图②中,已知AB=5,BE=3,则FD= ,△EFC的面积为 .(直接写结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求两位数的平方时,可以用“列竖式”的方法进行速算,求解过程如图1所示.
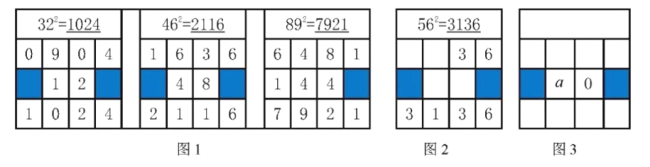
(1)仿照图1,在图2中补全![]() 的“竖式”;
的“竖式”;
(2)仿照图1,用“列竖式”的方法计算一个十位数字是![]() 的两位数的平方,过程部分如图3所示,则这个两位数为 (用含
的两位数的平方,过程部分如图3所示,则这个两位数为 (用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
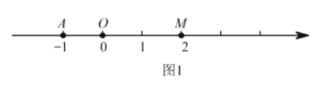
【题目】阅读下列材料:
我们给出如下定义:数轴上给定两点![]() ,
,![]() 以及一条线段
以及一条线段![]() ,若线段
,若线段![]() 的中点
的中点![]() 在线段
在线段![]() 上(点
上(点![]() 可以与点
可以与点![]() 或
或![]() 重合),则称点
重合),则称点![]() 与点
与点![]() 关于线段
关于线段![]() 径向对称.下图为点
径向对称.下图为点![]() 与点
与点![]() 关于线段
关于线段![]() 径向对称的示意图.
径向对称的示意图.

解答下列问题:
如图1,在数轴上,点![]() 为原点,点
为原点,点![]() 表示的数为-1,点
表示的数为-1,点![]() 表示的数为2.
表示的数为2.
(1)①点![]() ,
,![]() ,
,![]() 分别表示的数为-3,
分别表示的数为-3,![]() ,3,在
,3,在![]() ,
,![]() ,
,![]() 三点中, 与点
三点中, 与点![]() 关于线段
关于线段![]() 径向对称;
径向对称;
②点![]() 表示的数为
表示的数为![]() ,若点
,若点![]() 与点
与点![]() 关于线段
关于线段![]() 径向对称,则
径向对称,则![]() 的取值范围是 ;
的取值范围是 ;
(2)在数轴上,点![]() ,
,![]() ,
,![]() 表示的数分别是-5,-4,-3,当点
表示的数分别是-5,-4,-3,当点![]() 以每秒1个单位长度的速度向正半轴方向移动时,线段
以每秒1个单位长度的速度向正半轴方向移动时,线段![]() 同时以每秒3个单位长度的速度向正半轴方向移动.设移动的时间为
同时以每秒3个单位长度的速度向正半轴方向移动.设移动的时间为![]() (
(![]() )秒,问
)秒,问![]() 为何值时,线段
为何值时,线段![]() 上至少存在一点与点
上至少存在一点与点![]() 关于线段
关于线段![]() 径向对称.
径向对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:M=3a2+4ab -5a-6,N=a2-2ab-4
(1)化简:5M-(3N + 4M),结果用含a、b的式子表示.
(2)若式子5M-(3N + 4M)的值与字母a的取值无关,求b4+![]() M-
M-![]() N-
N-![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1) ∠DCF=![]() ∠BCD;(2)EF=CF;(3)S△CDF=S△CEF;(4)∠DFE=3∠AEF.其中正确结论的个数是( )
∠BCD;(2)EF=CF;(3)S△CDF=S△CEF;(4)∠DFE=3∠AEF.其中正确结论的个数是( )
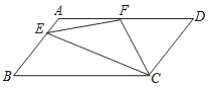
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
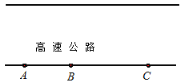
【题目】学习过绝对值之后,我们知道:|5-2|表示 5 与 2 的差的绝对值,实际上也可理解为 5 与 2 两数在数轴上所对应的两点之间的距离:|5+2|表示 5 与-2 的差的绝对值,实际上也可理解为 5 与-2 两数在数轴上所对应的两点之间的距离. 试探究解决以下问题:
⑴|x+6|可以理解为 与 两数在数轴上所对应的两点之间的距离;
⑵找出所有符合条件的整数 x,使|x+1|+|x-2|=3 成立;
⑶如图,在一条笔直的高速公路旁边依次有 A、B、C 三个城市,它们距高速公路起点的距离分别是 567km、689km、889km.现在需要在该公路旁建一个物流集散中心 P,请直接指出该物流集散中心 P 应该建设在何处,才能使得 P 到三个城市的距离之和最小?这个最小距离是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com