
【题目】某海尔专卖店春节期间,销售10台Ⅰ型号洗衣机和20台Ⅱ型号洗衣机的利润为4000元,销售20台Ⅰ型号洗衣机和10台Ⅱ型号洗衣机的利润为3500元.
(1)求每台Ⅰ型号洗衣机和Ⅱ型号洗衣机的销售利润;
(2)该商店计划一次购进两种型号的洗衣机共100台,其中Ⅱ型号洗衣机的进货量不超过Ⅰ型号洗衣机的进货量的2倍,问当购进Ⅰ型号洗衣机多少台时,销售这100台洗衣机的利润最大?最大利润是多少?
【答案】(1)每台I型电脑销售利润为100元,每台II型电脑的销售利润为150元;(2)商店购进34台I型电脑的销售利润最大,最大利润为13300元
【解析】
(1)设每台I型电脑销售利润为x元,每台II型电脑的销售利润为y元,然后根据利润4000元和3500元列出方程组,然后求解即可;
(2)设购进I型电脑x台,这100台电脑的销售总利润为w元.根据总利润等于两种电脑的利润之和列式整理即可得解;根据II型电脑的进货量不超过I型电脑的2倍列不等式求出x的取值范围,然后根据一次函数的增减性求出利润的最大值即可.
(1)设每台I型电脑销售利润为x元,每台II型电脑的销售利润为y元,根据题意得:![]() ,解得:
,解得:![]() .
.
答:每台I型电脑销售利润为100元,每台II型电脑的销售利润为150元.
(2)设购进I型电脑x台,这100台电脑的销售总利润为w元,根据题意得:w=100x+150(100﹣x),即w=﹣50x+15000,100﹣x≤2x,解得:x≥33![]() .
.
∵w=﹣50x+15000,∴w随x的增大而减小.
∵x为正整数,∴当x=34时,w取最大值,最大利润w=﹣50×34+15000=13300,则100﹣x=66,即商店购进34台I型电脑的销售利润最大,最大利润为13300元.


科目:初中数学 来源: 题型:
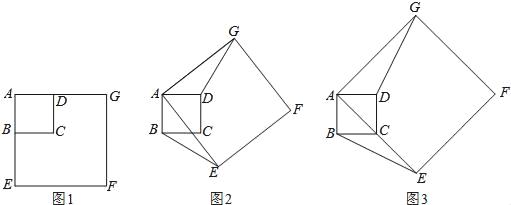
【题目】如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;(2)如图3,如果α=45°,AB=2,AE=4![]() ,求点G到BE的距离.
,求点G到BE的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师给爱好学习的小军和小俊提出这样一个问题:如图①,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.

【变式探究】如图③,当点P在BC延长线上时,其余条件不变,求证:PD﹣PE=CF;请运用上述解答中所积累的经验和方法完成下题:
【结论运用】如图④,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
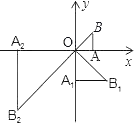
【题目】如图,在平面直角坐标系xoy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2,且A2O=2A1O,…,依此规律,得到等腰直角三角形A2018OB2018,则点A2018的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的动点,将
上的动点,将![]() 沿
沿![]() 折叠.
折叠.
(1)当点![]() 与点
与点![]() 重合时,如图1.若
重合时,如图1.若![]() ,
,![]() ,则
,则![]() 的周长为_____.
的周长为_____.
(2)定义:若在三角形中,期中一条边是另一条边的2倍,则称这个三角形为“倍边三角形”.当点![]() 与点
与点![]() 重合时,如图2.若
重合时,如图2.若![]() ,则
,则![]() 是倍边三角形吗?请说明理由.
是倍边三角形吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
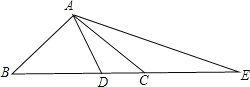
【题目】(1)如图,在在△ABC中,已知∠BAC=900,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,CE=CA,求∠DAE的度数;
(2)如果把(1)中的“AB=AC”条件去掉,其余条件不变,那么∠DAE的度数改变吗?为什么?
(3)如果把(1)中的“∠BAC=900”改成“∠BAC>900”其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设y是关于x的一次函数,其图象与y轴交点的纵坐标为﹣10,且当x=1时,y=﹣5.
(1)求该一次函数图象与坐标轴围成的三角形面积;
(2)当函数值为![]() 时,自变量的取值是多少?
时,自变量的取值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在 Rt ![]() 中,
中,![]() ,
, ![]() ,点
,点 ![]() 为射线
为射线 ![]() 上一点,连接
上一点,连接 ![]() ,过点
,过点 ![]() 作线段
作线段 ![]() 的垂线
的垂线 ![]() ,在直线
,在直线 ![]() 上,分别在点
上,分别在点 ![]() 的两侧截取与线段
的两侧截取与线段 ![]() 相等的线段
相等的线段 ![]() 和
和 ![]() ,连接
,连接 ![]() ,
,![]() .
.
(1)当点 ![]() 在线段
在线段 ![]() 上时(点
上时(点 ![]() 不与点
不与点 ![]() ,
,![]() 重合),如图1,
重合),如图1,
①请你将图形补充完整;
②线段 ![]() ,
,![]() 所在直线的位置关系为 ,线段
所在直线的位置关系为 ,线段 ![]() ,
,![]() 的数量关系为 ;
的数量关系为 ;

(2)当点 ![]() 在线段
在线段 ![]() 的延长线上时,如图2,
的延长线上时,如图2,
①请你将图形补充完整;
②在(1)中②问的结论是否仍然成立?如果成立请进行证明,如果不成立,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com