
【题目】在一个不透明的盒子里装有4个分别标有:﹣1、﹣2、0、1的小球,它们的形状、大小完全相同,小芳从盒子中随机取出一个小球,记下数字为x,作为点M的横坐标:小华在剩下的3个小球中随机取出一个小球,记下数字为y,作为点M的纵坐标.
(1)用画树状图或列表的方式,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=![]() 的图象上的概率.
的图象上的概率.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B两点,与y轴交于点C,对称轴为x=1.
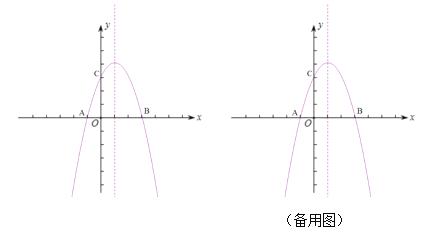
(1)求抛物线的函数表达式;
(2)在抛物线的对称轴上求一点P,使点P到点A的距离与到点C的距离之和最小,并求出此时点P的坐标;
(3)是否存在过A,B两点的抛物线,其顶点M关于x轴的对称点为N,使得四边形AMBN为正方形?若存在,请直接写出此抛物线的函数表达式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
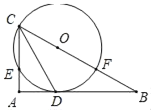
【题目】如图,Rt△ABC中,∠A=90°,CD平分∠ACB交AB于点D,O是BC上一点,经过C、D两点的⊙O分别交AC、BC于点E、F,AD=![]() ,∠ADC=60°,则劣弧
,∠ADC=60°,则劣弧![]() 的长为_____.
的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点B的坐标为(1,0)其图象如图所示,下列结论:①abc>0;②2a﹣b=0;③一元二次方程ax2+bx+c=0的两个根是﹣3和1;④当y>0时,﹣3<x<1;⑤当x>0时,y随x的增大而增大:⑥若点E(﹣4,y1),F(﹣2,y2),M(3,y3)是函数图象上的三点,则y1>y2>y3,其中正确的有( )个
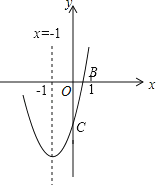
A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以每件60元的价格购进一批货物,零售价为每件80元时,可以卖出100件(按相关规定零售价不能超过80元).如果零售价在80元的基础上每降价1元,可以多卖出10件,当零售价在80元的基础上降价x元时,能获得2160元的利润,根据题意,可列方程为( )
A.x(100+10x)=2160B.(20﹣x)(100+10x)=2160
C.(20+x)(100+10x)=2160D.(20﹣x)(100﹣10x)=2160
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O,再任意找出圆O的一条直径标记为AB(如图1),测量出AB=4分米;②将圆环进行翻折使点B落在圆心O的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C、D(如图2);③用一细橡胶棒连接C、D两点(如图3);④计算出橡胶棒CD的长度.
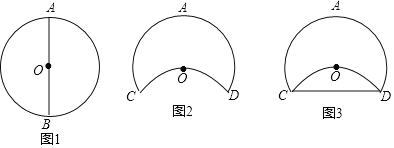
小明计算橡胶棒CD的长度为( )
A.2![]() 分米B.2
分米B.2![]() 分米C.3
分米C.3![]() 分米D.3
分米D.3![]() 分米
分米
查看答案和解析>>
科目:初中数学 来源: 题型:
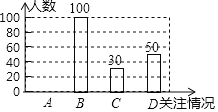
【题目】2019年2月18日,“时代楷模”、伏牛山里的好教师﹣﹣张玉滚当选“感动中国”2018年度人物,在中原大地引起强烈反响.为了解学生对张玉滚事迹的知晓情况,某数学课外兴趣小组在本校学生中开展了专题调查活动,随机抽取了部分学生进行问卷调查,根据学生的答题情况,将结果分为A,B,C,D四类,将调查的数据整理后绘制成如下统计表及条形统计图(均不完整):
关注情况 | 频数 | 频率 |
A.非常了解 | m | 0.1 |
B.比较了解 | 100 | 0.5 |
C.基本了解 | 30 | n |
D.不太了解 | 50 | 0.25 |
根据以上信息解答下列问题:
(1)在这次抽样调查中,一共抽查了 名学生;
(2)统计表中,m= ,n= ;
(3)请把条形统计图补充完整;
(4)该校共有学生1500名,请你估算该校学生中对张玉滚事迹“非常了解“和“比较了解”的学生共有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
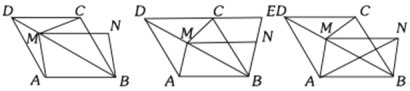
【题目】如图1,在菱形ABCD中,AB=![]() ,∠BCD=120°,M为对角线BD上一点(M不与点B、D重合),过点MN∥CD,使得MN=CD,连接CM、AM、BN.
,∠BCD=120°,M为对角线BD上一点(M不与点B、D重合),过点MN∥CD,使得MN=CD,连接CM、AM、BN.
(1)当∠DCM=30°时,求DM的长度;
(2)如图2,延长BN、DC交于点E,求证:AM·DE=BE·CD;
(3)如图3,连接AN,则AM+AN的最小值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com