
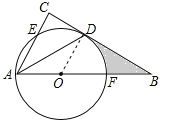
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接OD,证明OD∥AC,即可证得∠ODB=90°,从而证得BC是圆的切线;
(2)在直角三角形OBD中,设OF=OD=x,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为圆的半径,求出圆心角的度数,直角三角形ODB的面积减去扇形DOF面积即可确定出阴影部分面积.
试题解析:(1)BC与⊙O相切.
证明:连接OD.∵AD是∠BAC的平分线,∴∠BAD=∠CAD.又∵OD=OA,∴∠OAD=∠ODA,∴∠CAD=∠ODA,∴OD∥AC,∴∠ODB=∠C=90°,即OD⊥BC.又∵BC过半径OD的外端点D,∴BC与⊙O相切.
(2)设OF=OD=x,则OB=OF+BF=x+2,由勾股定理得:OB2=OD2+BD2,即(x+2)2=x2+12,解得:x=2,即OD=OF=2,∴OB=2+2=4,∵Rt△ODB中,OD=![]() OB,∴∠B=30°,∴∠DOB=60°,∴S扇形AOB=
OB,∴∠B=30°,∴∠DOB=60°,∴S扇形AOB=![]() =
=![]() ,则阴影部分的面积为S△ODB﹣S扇形DOF=
,则阴影部分的面积为S△ODB﹣S扇形DOF=![]() ×2×
×2×![]() ﹣
﹣![]() =
=![]() .故阴影部分的面积为
.故阴影部分的面积为![]() .
.


科目:初中数学 来源: 题型:
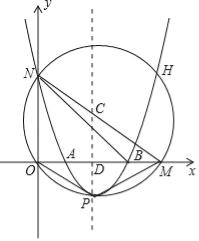
【题目】如图所示,在平面直角坐标系中,⊙C经过坐标原点O,且与x轴,y轴分别相交于M(4,0),N(0,3)两点.已知抛物线开口向上,与⊙C交于N,H,P三点,P为抛物线的顶点,抛物线的对称轴经过点C且垂直x轴于点D.
(1)求线段CD的长及顶点P的坐标;
(2)求抛物线的函数表达式;
(3)设抛物线交x轴于A,B两点,在抛物线上是否存在点Q,使得S四边形OPMN=8S△QAB,且△QAB∽△OBN成立?若存在,请求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,∠ACB=30°,BC=3,分别过点B,C作BE∥AC,CE∥BD,且BE,CE相交于点E. 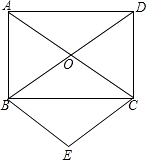
(1)求AB,AC的长;
(2)判断四边形BOCE的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续正整数按如下个规律排列
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | ……… | |
第一行 | 1 | 2 | 3 | 4 | ||
第二行 | 8 | 7 | 6 | 5 | ||
第三行 | 9 | 10 | 11 | 12 | ||
第四行 | 16 | 15 | 14 | 13 | ||
第五行 | 17 | 18 | 19 | 20 | ||
……… |
若正整数2019位于第a行、第b列,则a+b=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数![]() (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下: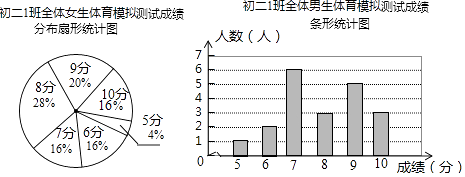
初二1班体育模拟测试成绩分析表
平均分 | 方差 | 中位数 | 众数 | |
男生 | 2 | 8 | 7 | |
女生 | 7.92 | 1.99 | 8 |
根据以上信息,解答下列问题:
(1)这个班共有男生人,共有女生人;
(2)补全初二1班体育模拟测试成绩分析表;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com