
分析 根据解三元一次方程组的方法可以解答此方程,注意观察方程的特点,巧妙变形解答方程.
解答 解:$\left\{\begin{array}{l}{\frac{x-1}{2}=\frac{-y+3}{4}=\frac{2z-3}{5}}\\{z-x=1}\end{array}\right.$
∴$\left\{\begin{array}{l}{\frac{x-1}{2}=\frac{-y+3}{4}}&{①}\\{\frac{x-1}{2}=\frac{2z-3}{5}}&{②}\\{z-x=1}&{③}\end{array}\right.$
由③,得
z=x+1④,
将④代入②,得
x=3,
将x=3代入④,得
z=4,
将x=3代入①,得
y=-1
故原方程组的解是$\left\{\begin{array}{l}{x=3}\\{y=-1}\\{z=4}\end{array}\right.$.
点评 本题考查解三元一次方程组,解题的关键是明确解三元一次方程组的方法.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
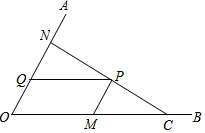 如图,C为∠AOB的边OB上一点,OC=10,N为边OA上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OB交OA于点Q,PM∥OA交OB于点M.
如图,C为∠AOB的边OB上一点,OC=10,N为边OA上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OB交OA于点Q,PM∥OA交OB于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某农场要建一个长方形的养兔场,兔场的两边靠墙,两堵墙互相垂直,长度足够长,另两边用木栏围成,木栏总长20m.
如图,某农场要建一个长方形的养兔场,兔场的两边靠墙,两堵墙互相垂直,长度足够长,另两边用木栏围成,木栏总长20m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
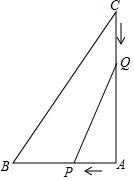 如图,在△ABC中,已知∠BAC=90°,AB=6cm,AC=8cm,点P从点A出发以1cm/s的速度移动到点B,点Q从点C出发以2cm/s的速度移动到点A.
如图,在△ABC中,已知∠BAC=90°,AB=6cm,AC=8cm,点P从点A出发以1cm/s的速度移动到点B,点Q从点C出发以2cm/s的速度移动到点A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com