

分析 (1)如图2中,连接PQ.只要证明△PBQ∽△CBA,得$\frac{PB}{CB}$=$\frac{BQ}{BA}$,列出方程即可解决问题.
(2)作QH⊥AB于H.根据y=S△ABC-S△PBQ,构建二次函数,理由二次函数的性质即可解决问题.
(3)分两种情形讨论①∠B=∠C,当$\frac{BP}{CA}$=$\frac{BQ}{CQ}$时,△PBQ∽△ACQ,②当$\frac{BP}{CQ}$=$\frac{BQ}{CA}$时,△PBQ∽△QCA,分别列出方程即可解决问题.
解答 解:(1)如图2中,连接PQ.
∵四边形APQC恰好内接于一个圆,
∴∠PQC+∠PAC=180°,∵∠PAC=90°,
∴∠PQC=90°,
∵∠B=∠B,∠BQP=∠A=90°,
∴△PBQ∽△CBA,
∴$\frac{PB}{CB}$=$\frac{BQ}{BA}$,
∴$\frac{4-t}{4\sqrt{2}}$=$\frac{\sqrt{2}t}{4}$,
∴t=$\frac{4}{3}$s.
故答案为$\frac{4}{3}$
(2)如图1中,作QH⊥AB于H.
y=S△ABC-S△PBQ=$\frac{1}{2}$×4×4=$\frac{1}{2}$•PB•QH=8-$\frac{1}{2}$(4-t)•t=$\frac{1}{2}$t2-2t+8=$\frac{1}{2}$(t-2)2+6.
∵$\frac{1}{2}$>0,
∴t=2时,y有最小值.最小值为6.
(3)如图3中,
①∵∠B=∠C,
∴当$\frac{BP}{CA}$=$\frac{BQ}{CQ}$时,△PBQ∽△ACQ,
∴$\frac{4-t}{4}$=$\frac{\sqrt{2}t}{4\sqrt{2}-\sqrt{2}t}$,
∴t=6-2$\sqrt{5}$或6+2$\sqrt{5}$(舍弃).
②当$\frac{BP}{CQ}$=$\frac{BQ}{CA}$时,△PBQ∽△QCA,
∴$\frac{4-t}{4\sqrt{2}-\sqrt{2}t}$=$\frac{\sqrt{2}t}{4}$,
∴t=2或4(舍弃),
综上所述,t=(6-2$\sqrt{5}$)s或2s时,△PBQ与△AQC相似.
点评 本题考查相似三角形综合题、圆的有关知识、一元二次方程等知识,解题的关键是灵活运用所学知识,学会用分类讨论的思想思考问题,学会用 方程的思想思考问题,把问题转化为方程解决,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 3 s | B. | 4 s | C. | 5 s | D. | 6 s |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
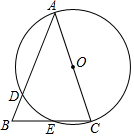 如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交AB于点E.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
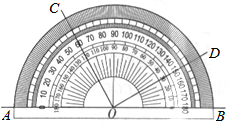 如图所示,用量角器度量一些角的度数.下列结论中正确的是( )
如图所示,用量角器度量一些角的度数.下列结论中正确的是( )| A. | ∠BOC=60° | B. | ∠COD=150° | ||
| C. | ∠AOC与∠BOD的大小相等 | D. | ∠AOC与∠BOD互余 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
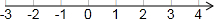
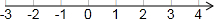
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com