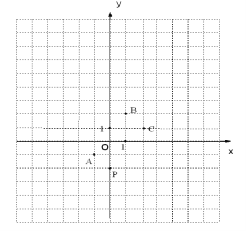
【题目】如图，在平面直角坐标系中，一颗棋子从点P处开始依次关于点A、B、C作循环对称跳动，即第一次跳到点P关于点A的对称点M处，接着跳到点M关于点B的对称点N处，第三次再跳到点N关于点C的对称点处，…．如此下去。
（1）在图中画出点M、N，并写出点M、N的坐标：
（2）求经过第2010次跳动之后，棋子落点的位置。
【答案】(1) M（-2，0），N（4，4）；(2)（0，-2）.
【解析】
（1）点P关于点A的对称点M，即是连接PA延长到M使PA=AM，所以M的坐标是M（-2，0），点M关于点B的对称点N处，即是连接PB延长到N使PB=BN，所以N的坐标是N（4，4）；
（2）棋子跳动3次后又回点P处，利用这个循环的规律就可以得到棋子落点处的坐标．
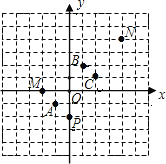
解：（1）首先发现点P的坐标是（0，-2），第一次跳到点P关于A点的对称点M处是（-2，0），跳到点M关于点B的对称点N处是（4，4）；
（2）由（1）得出：则第三次再跳到点N关于点C的对称点处是（0，-2）…，发现3次一循环．又2010÷3=670，则第2010次跳动之后，棋子落点的坐标与点P坐标相同，落在了（0，-2）处．
世纪百通优练测系列答案
百分学生作业本题练王系列答案科目：初中数学 来源： 题型：
【题目】某糕点厂中秋节前要制作一批盒装月饼，每盒装1个大月饼和7个小月饼，制作1个大月饼要用0.06kg面粉，1个小月饼要用0.015kg面粉，现共有面粉330kg，制作两种月饼各用多少kg面粉时，才能使生产的大小月饼刚好配套成盒？最多能生产多少盒月饼？
查看答案和解析>>
科目：初中数学 来源： 题型：
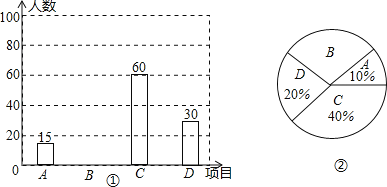
【题目】为推广阳光体育“大课间”活动，我市某中学决定在学生中开设A：实心球．B：立定跳远，C：跳绳，D：跑步四种活动项目．为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如图①②的统计图．请结合图中的信息解答下列问题：
（1）在这项调查中，共调查了多少名学生？
（2）请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比，并将两个统计图补充完整．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线AB经过x轴上的点M，与反比例函数y= 
（x＞0）的图象相交于点A（1，8）和B（m，n），其中m＞1，AC⊥x轴于点C，BD⊥y轴于点D，AC与BD交于点P．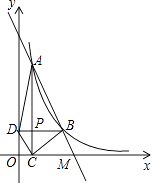
（1）求k的值；
（2）若AB=2BM，求△ABD的面积；
（3）若四边形ABCD为菱形，求直线AB的函数解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
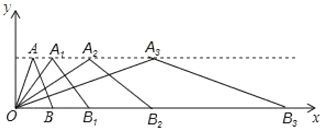
【题目】如图，在平面直角坐标系中，第一次将三角形
变换成三角形
，第二次将三角形变换成三角形
，第三次将三角形变换成三角形
，已知
，
，
，
，
，
，
，
．
（1）观察每次变换前后的三角形，找出规律，按这些变换规律将三角形变换成三角形
，求
和
的坐标；
（2）若按第（1）题的规律将三角形进行了
次变换，得到三角形
，请推测
和
的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
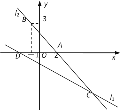
【题目】如图，直线l1的函数关系式为y＝－
x－1，且l1与x轴交于点D，直线l2经过点A（2，0），B（－1，3），直线l1与l2交于点C．
（1）求直线l2的函数关系式；
（2）点C的坐标为 ；
（3）求△ADC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，O为直线AB上一点，∠AOC＝50°，OD平分∠AOC，∠DOE＝90°.
(1)请你数一数，图中有多少个小于平角的角；
(2)求出∠BOD的度数；
(3)请通过计算说明OE是否平分∠BOC.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AB=3cm，BC=6cm.点P从点D出发向点A运动，运动到点A即停止；同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时，四边形ABQP是矩形；
当t为何值时，四边形AQCP是菱形；
分别求出（2）中菱形AQCP的周长和面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com