
 如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO.下列结论:
如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO.下列结论:分析 根据全等三角形的性质得出∠AOB=∠AOD=90°,OB=OD,再根据全等三角形的判定定理得出△ABC≌△ADC,进而得出其它结论.
解答 解:∵△ABO≌△ADO,
∴∠AOB=∠AOD=90°,OB=OD,
∴AC⊥BD,故①正确;
∵四边形ABCD的对角线AC、BD相交于点O,
∴∠COB=∠COD=90°,
在△ABC和△ADC中,
$\left\{\begin{array}{l}{OB=OD}\\{∠BOC=∠DOC}\\{OC=OC}\end{array}\right.$,
∴△ABC≌△ADC(SAS),故③正确
∴BC=DC,故②正确;
故答案为①②③.
点评 本题考查了全等三角形的判定和性质,掌握全等三角形的判定方法:SSS,SAS,ASA,AAS,以及HL,是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则$\frac{{S}_{正方形MNPQ}}{{S}_{正方形AEFG}}$的值等于$\frac{8}{9}$.
如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则$\frac{{S}_{正方形MNPQ}}{{S}_{正方形AEFG}}$的值等于$\frac{8}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
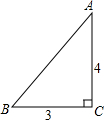 如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处.这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是( )
如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处.这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是( )| A. | c>a>b | B. | b>a>c | C. | c>b>a | D. | b>c>a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
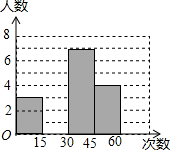 在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:| 分 组 | 频数 | 频率 |
| 第一组(0≤x<15) | 3 | 0.15 |
| 第二组(15≤x<30) | 6 | a |
| 第三组(30≤x<45) | 7 | 0.35 |
| 第四组(45≤x<60) | b | 0.20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是( )
如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是( )| A. | AB=AE | B. | AB=BE | C. | AE=BE | D. | AB=AC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.402×10-5 | B. | 4.02×10-6 | C. | 4.02×10-7 | D. | 40.2×10-7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com