
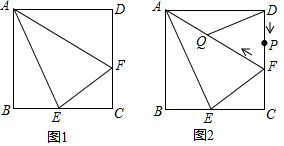
���� ��1����AE��EF��֪����BAE=��CEF���Ӷ��á�ABE�ס�ECF��
��2������E��EH��AF�ڵ�H���ɡ�ABE�ס�AEF��֪AEƽ�֡�BAF�����ý�ƽ���ߵ����ʼ��ɵó�BE=CE��
��3���������֪PD=QF=t������ΪPD=QD������QF=QD�����õ��������ε����ߺ�һ�������t��ֵ��
��� ֤������1����AE��EF��
���AEB+��FEC=90�㣬
�ߡ�BAE+��AEB=90�㣬
���BAE=��FEC��
�ߡ�B=��C=90�㣬
���ABE�ס�ECF��
��2������E��EH��AF�ڵ�H��
�ߡ�ABE�ס�AEF��
��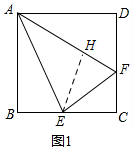 ��BAE=��EAH��
��BAE=��EAH��
��AEƽ�֡�BAH��
��EB��AB��EH��AF��
��BE=EH��
�ߡ�HEF+��AEH=90�㣬
��EAH+��AEH=90�㣬
���HEF=��EAH��
���HEF=��EAH=��BAE=��FEC��
��EFƽ�֡�HEC��
��EH��AF��EC��CD��
��EH=CE��
��BE=EH=CE��
��3�� �ɣ�1����֪����ABE�ס�ECF
�ɣ�1����֪����ABE�ס�ECF
��$\frac{BE}{AB}=\frac{CF}{CE}$��
��CF=1��
��DF=3��
��AD=4��
���ɹ��ɶ�������ã�AF=5��
�������֪��PD=FQ=t��
��QD=PDʱ��
��ʱ��QD=FQ��
����Q��QG��DF�ڵ�G��
��GF=$\frac{1}{2}$DF=$\frac{3}{2}$��
��cos��AFD=$\frac{DF}{AF}=\frac{FG}{QF}$��
��$\frac{3}{5}=\frac{\frac{3}{2}}{t}$��
��t=$\frac{5}{2}$��
��t=$\frac{5}{2}$ʱ��PD=QD��
���� ���⿼�������ۺ��⣬�漰���ɶ�������������κ��������������ε��������ж������������ε����ʵ�֪ʶ���ۺϳ̶Ƚϸߣ�


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����ƽ��ֱ������ϵ�У�����������y=-2x��ͼ���뷴��������y=$\frac{k}{x}$��ͼ���һ������ΪA��-1��n����
��ͼ��ʾ����ƽ��ֱ������ϵ�У�����������y=-2x��ͼ���뷴��������y=$\frac{k}{x}$��ͼ���һ������ΪA��-1��n�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
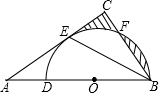 ��ͼ���ڡ�ABC�У���C=90�㣬BE�ǽ�ƽ���ߣ���D��AB���ϣ���DBΪֱ���İ�ԲO������E����BC�ڵ�F��
��ͼ���ڡ�ABC�У���C=90�㣬BE�ǽ�ƽ���ߣ���D��AB���ϣ���DBΪֱ���İ�ԲO������E����BC�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com