
P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若 ,
,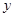 都是整数,则这样的点共有( )
都是整数,则这样的点共有( )
A.4个 B.8个 C.12个 D.16个
C
【解析】
试题分析:应分为两种情况:①若这个点在坐标轴上,那么有四个;②若这个点在象限内,由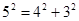 ,可知在每个象限有两个,总共12个.
,可知在每个象限有两个,总共12个.
分为两种情况;
①若这个点在坐标轴上,那么有四个,它们是(0,5),(5,0),(-5,0),(0,-5);
②若这个点在象限内,
∵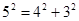 ,而P都是整数点,
,而P都是整数点,
∴这样的点有8个,分别是(3,4),(3,-4),(-3,4),(-3,-4)),(4,3),(4,-3),(-4,3),(-4,-3).
∴共12个,故选C.
考点:此题主要考查了点与圆的位置关系及勾股定理
点评:解答本题的关键是由题意得出分为两种不同的情况,再由勾股定理解决问题.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
 (2012•昆山市二模)如图,直线l的解析式为y=
(2012•昆山市二模)如图,直线l的解析式为y=
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•兰州)如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,∠AOB=45°,点P在x轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设P(x,0),则x的取值范围是
(2012•兰州)如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,∠AOB=45°,点P在x轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设P(x,0),则x的取值范围是| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com