
分析 (1)设“阶梯数”t的百位为x,相邻两数的差为k,则t=$\overline{a(a+k)a}$,可得M=a+a=2a,N=a+k,根据P(t)=12,得到关于k的方程,可求k=6,再根据Q(t)=3a+6为一个完全平方数,其中1≤a≤9,可求3a+6=9,16,25,可求a=1,从而得到这个三位数;
(2)设某五位阶梯数为$\overline{a(a+k)(a+2k)(a+k)a}$,根据$\frac{t}{4}$=$\frac{11111a+1210k}{4}$=2778a+302k+$\frac{2k-a}{4}$,
可得2k-a是4的倍数,根据M=3a+2k,N=2A+2K,可得Q(t)=M+N=5a+4k,则$\frac{5a+4k-2}{4}$=k+a+$\frac{a-2}{4}$,可得a-2是4的倍数,根据完全平方数的定义得到a=2,6,再分两种情况求得t的值,进一步得到该五位“阶梯数”t的最大值和最小值.
解答 解:(1)设“阶梯数”t的百位为x,相邻两数的差为k,则t=$\overline{a(a+k)a}$,
∴M=a+a=2a,N=a+k,
∴P(t)=2N-M=2(a+k)-2a=2k=12,
∴k=6,
∵Q(t)=M+N=2a+a+k=3a+6为一个完全平方数,其中1≤a≤9,
∴9≤3a+6≤33,
∴3a+6=9,16,25,
∴a=1,
∴t=171;
(2)设某五位阶梯数为$\overline{a(a+k)(a+2k)(a+k)a}$,
∵$\frac{t}{4}$=$\frac{11111a+1210k}{4}$=2778a+302k+$\frac{2k-a}{4}$,
∴2k-a是4的倍数,
∵M=3a+2k,N=2A+2K,
∴Q(t)=M+N=5a+4k,
∴$\frac{5a+4k-2}{4}$=k+a+$\frac{a-2}{4}$,
∴a-2是4的倍数,
∵1≤a≤9,
∴-1≤a-2≤7,
∴a-2=0,4,
∴a=2,6
当a=2时,$\frac{2k-2}{4}$为整数且0≤2+2k≤9,
∴-1≤k≤$\frac{7}{2}$,
∴k=±1,3,
所以t=21012,23432,25852;
当a=6时,$\frac{2k-6}{4}$为整数且0≤6+2k≤9,
∴-3≤k≤$\frac{3}{2}$,
∴k=±1,-3,
所以t=63036,65456,67876.
所以该五位“阶梯数”t的最大值是67876,最小值是21012.
点评 考查了完全平方数,解题的关键是弄清楚“阶梯数”的定义,从而写出符合题意的数.


科目:初中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ②④ | C. | ①③ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (6,7) | B. | (7,8) | C. | (7,9) | D. | (6,9) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
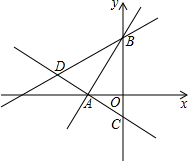 如图,在平面直角坐标系中,已知点A(-$\sqrt{3}$,0),B(0,3),C(0,-1)三点.
如图,在平面直角坐标系中,已知点A(-$\sqrt{3}$,0),B(0,3),C(0,-1)三点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com