
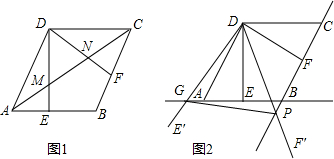
分析 (1)连接BD,证明△ABD为等边三角形,根据等腰三角形的三线合一得到AE=EB,根据相似三角形的性质解答即可;
(2)分∠EDF顺时针旋转和逆时针旋转两种情况,根据旋转变换的性质解答即可.
解答 (1)证明:如图1,连接BD, 交AC于O,
交AC于O,
在菱形ABCD中,∠BAD=60°,AD=AB,
∴△ABD为等边三角形,
∵DE⊥AB,
∴AE=EB,
∵AB∥DC,
∴$\frac{AM}{MC}$=$\frac{AE}{DC}$=$\frac{1}{2}$,
同理,$\frac{CN}{AN}$=$\frac{1}{2}$,
∴MN=$\frac{1}{3}$AC;
(2)解:∵AB∥DC,∠BAD=60°,
∴∠ADC=120°,又∠ADE=∠CDF=30°,
∴∠EDF=60°,
当∠EDF顺时针旋转时,
由旋转的性质可知,∠EDG=∠FDP,∠GDP=∠EDF=60°,
DE=DF=$\sqrt{3}$,∠DEG=∠DFP=90°,
在△DEG和△DFP中,
$\left\{\begin{array}{l}{∠GDE=∠PDF}\\{∠DEG=∠DFP}\\{DE=DF}\end{array}\right.$,
∴△DEG≌△DFP,
∴DG=DP,
∴△DGP为等边三角形,
∴△DGP的面积=$\frac{\sqrt{3}}{4}$DG2=3$\sqrt{3}$,
解得,DG=2$\sqrt{3}$,
则cos∠EDG=$\frac{DE}{DG}$=$\frac{1}{2}$,
∴∠EDG=60°,
∴当顺时针旋转60°时,△DGP的面积等于3$\sqrt{3}$,
同理可得,当逆时针旋转60°时,△DGP的面积也等于3$\sqrt{3}$,
综上所述,将△EDF以点D为旋转中心,顺时针或逆时针旋转60°时,△DGP的面积等于3$\sqrt{3}$.
点评 本题考查的是菱形的性质和旋转变换,掌握旋转的性质:①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后的图形全等是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
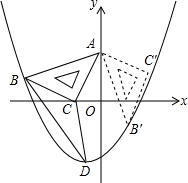 如图,在平面直角坐标系中,将一块腰长为5的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点B在抛物线y=ax2+ax-2上.
如图,在平面直角坐标系中,将一块腰长为5的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点B在抛物线y=ax2+ax-2上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
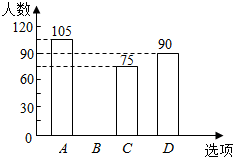 某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:| 选项 | 方式 | 百分比 |
| A | 唱歌 | 35% |
| B | 舞蹈 | a |
| C | 朗诵 | 25% |
| D | 器乐 | 30% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=x2-(2k+1)x+k2+k(k>0)
已知二次函数y=x2-(2k+1)x+k2+k(k>0)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “打开电视,正在播放《新闻联播》”是必然事件 | |
| B. | “x2<0(x是实数)”是随机事件 | |
| C. | 掷一枚质地均匀的硬币10次,可能有5次正面向上 | |
| D. | 为了了解夏季冷饮市场上冰淇淋的质量情况,宜采用普查方式调查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com