
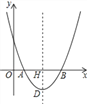
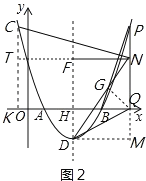
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬������y=ax2��10ax+16a��a��0����x����A��B���㣬�����ߵĶ���ΪD���Գ�����x�ύ�ڵ�H����AB=2DH��
��1����a��ֵ��
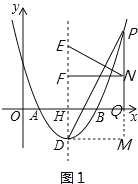
��2����P�ǶԳ����Ҳ��������ϵĵ㣬����PD��PQ��x���ڵ�Q����N���߶�PQ�ϵĵ㣬����N��NF��DH�ڵ�F��NE��PD��ֱ��DH�ڵ�E�����߶�EF�ij���
��3���ڣ�2���������£�����DN��DQ��PB����DN=2QN��NQ��3����2��NDQ+��DNQ=90��ʱ����NC��PB���Գ��������������ڵ�C�����C�����꣮
���𰸡���1��![]() ����2��3����3����C����1��9������
����2��3����3����C����1��9������
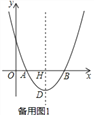
�������������������1������y=ax2-10ax+16a������õ�y=0ʱ��x��ֵ���Ӷ�������õ�A��B�����꣬�������ߵĶ���ΪD���Գ�����x�ύ�ڵ�H����AB=2DH���Ӷ��������a��ֵ��
��2��������֪����������Ӧ��ͼ�Σ�Ȼ�����������Ŀ�е�������ϵ��ͨ�������ο������EF�ij���
��3������������Ի�����Ӧ��ͼ�Σ�Ȼ�������Ŀ�еĹ�ϵ���������������ƣ����仯������õ�C�����꣮
�����������1����y=0����x=2��x=8�����A��2��0����B��8��0������AB=6��
��AB=2DH����DH=3��
��OH=2+![]() ����D��5����3�����ੁ3=a��52��10a��5+16a����a=
����D��5����3�����ੁ3=a��52��10a��5+16a����a=![]() ��
��
��2����ͼ1������D��PQ�Ĵ��ߣ���PQ���ӳ����ڵ�M��
��NE��PD�����DPN+��PNE=90�㣬��NF��DE�����FEN+��FNE=90�㣬
�֡�DH��x�ᣬPQ��x�ᣬ��DE��PQ�����FEN=��PNE�����DPM=��ENF�����EFN�ס�DMP��
��![]() �����P��t��
�����P��t�� ![]() ������FN=DM=t��5��PM=
������FN=DM=t��5��PM=![]() +3��������EF=3��
+3��������EF=3��
��3����ͼ2����QG��DN�ڵ�G����DF��PQ�����FDN=��DNQ����2��NDQ+��DNQ=90�㣬
��2��NDQ+��FDN=90�㣬�ߡ�FDM=90�㣬���NDM=2��NDQ�����NDQ=��MDQ����QG=QM=DH=3��
��QN=m����DN=2m����sin��DNM=![]() ��sin��QNG=
��sin��QNG=![]() ��sin��DNM=sin��QNG��
��sin��DNM=sin��QNG��
��![]() ����DM=6=DG����OQ=5+6=11��
����DM=6=DG����OQ=5+6=11��
���P���������ǣ� ![]() =9�����P��11��9����
=9�����P��11��9����
��NG=2m��6����Rt��NGQ��QG2+NG2=QN2��
��32+��2m��6��2=m2���ã�m=3���ᣩ��m=5��
��C��n�� ![]() ������CK��x���ڵ�K����NF��CK�ڵ�K����CT=
������CK��x���ڵ�K����NF��CK�ڵ�K����CT=![]() ��NT=11��n��
��NT=11��n��
��P��11��9������BQ=11��8=3��PQ=9��
��CN��PB��PQ��CK��PQ��x�ᣬ ���CTN�ס�BQP��
��![]() �� ��
�� ��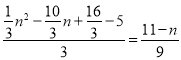 �� ��ã�n=��1��n=10����ȥ����
�� ��ã�n=��1��n=10����ȥ����
���C����1��9����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�DZ߳�Ϊ6�ĵȱ������Σ���D��E�ֱ��DZ�AB��AC���е㣬����ADE�Ƶ�A��ת��BD��CE���ڵ�ֱ�߽��ڵ�F��
(1)��ͼ(2)��ʾ������ADE�Ƶ�A��ʱ����ת������ת�Dz�����60������CFB�Ķ����Ƕ��٣�˵��������ɣ�
(2)����ADE�Ƶ�A��תʱ������BCFΪֱ�������Σ�����߶�BF�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
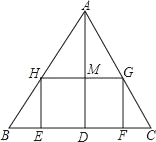
����Ŀ����ͼ����ABC��һ����������ε�ӲֽƬ��AD�DZ�BC�ϵĸߣ�BC=40cm��AD=30cm��������ӲֽƬ����һ����HG�ǿ�HE��2���ľ���EFGH��ʹ����һ��EF��BC�ϣ�����G��H�ֱ���AC��AB�ϣ�AD��HG�Ľ���ΪM��
��1����֤�� ![]() ��
��
��2�����������EFGH���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ͼ����y�ᡢx��ֱ���A��B����
ͼ����y�ᡢx��ֱ���A��B����
��1�����A��B����͡�BAO����
��2����C��D�ֱ����߶�OA��AB��һ���㣨����˵��غϣ�����CD=DA�����߶�OC�ij���Ϊx ,![]() ,�����y����x�ĺ�����ϵʽ�Լ�������
,�����y����x�ĺ�����ϵʽ�Լ�������
��3����C��D�ֱ�������OA������BA��һ���㣬��CD=DA������ODBΪ����������ʱ����C�����꣨�ڣ�3��С��ֱ��д����������ʹ𰸣����ù��̣�



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�У�E��F�ǶԽ���BD�ϵ����㣬�������һ��������ʹ��ABE�ա�CDF�������ӵ���������Ϊ��������

A. BE=DF B. BF=DE C. AE=CF D. ��1=��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ϵ�A��B����ֱ��Ӧ����a��b����a��b����|4a-b|+��a-4��2=0
![]()
��1��a= ��b= ���������������A��B���㣻
��2������P�ӵ�A��������ÿ��3����λ������x���������˶������˶�ʱ��Ϊ����ʱ����P����A�ľ����ǵ�P����B�����2����
��3�������ϻ���һ��C������Ϊ30������P�͵�Qͬʱ�ӵ�A�͵�B�������ֱ���ÿ��3����λ���Ⱥ�ÿ��1����λ���ȵ��ٶ���C���˶���P�㵽��C�����������ͬ�����ٶȷ��أ��˶����յ�A�����P�͵�Q�˶�������ʱ��P��Q����֮��ľ���Ϊ4�������ʱ��Q��Ӧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣨1��![]() ��2��
��2��![]()
��3��![]() ��4��
��4��![]()
��5��![]() ��6��
��6��![]()
��7��![]() ��8��
��8��![]()
��9��![]() ��10��
��10��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽������������������֮��ľ������������Ӧ�����Ĺ�ϵ��
![]()
��1�������A��ʾ��5������A�������ƶ�4����λ���ȵ����B����ô��B��ʾ������������A��B�����ľ��������� ��
�����A��ʾ����2������A�����ƶ�5����λ���ȵ����B����ô��B��ʾ������������A��B�����ľ������� ��
��2�����֣��������ϣ������M��Ӧ������m����N��Ӧ������n����ô��M���N֮��ľ���ɱ�ʾΪ�� ����m��n��ʾ����m��n����
��3��Ӧ���������㷢�ֵĽ��۽���������⣺�����ϱ�ʾx�ͩ�2������P��Q֮��ľ�����3����x=���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
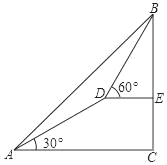
����Ŀ����ͼ��������Ա��ɽ��A�����ɽ��B������Ϊ45������������Ϊ30����ɽ��ǰ��1000����D������D�����ɽ��B������Ϊ60�㣬��ɽ�ĸ߶ȣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com