
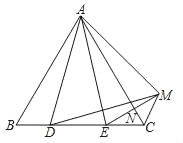
【题目】如图,△ABC是等边三角形,D,E是BC上的两点,且BD=CE,连接AD、AE,将△AEC沿AC翻折,得到△AMC,连接EM交AC于点N,连接DM.以下判断:①AD=AE,②△ABD≌△DCM,③△ADM是等边三角形,④CN=![]() EC中,正确的是_____.
EC中,正确的是_____.
【答案】①③④.
【解析】
由等边三角形的性质得出AB=AC,∠B=∠BAC=∠ACE=60![]() ,由SAS证得△ABD≌△ACE,得出∠BAD=∠CAE,AD=AE,由折叠的性质得CE=CM=BD,AE=AM=AD,∠CAE=∠CAM=∠BAD,推出∠DAM=∠BAC=60
,由SAS证得△ABD≌△ACE,得出∠BAD=∠CAE,AD=AE,由折叠的性质得CE=CM=BD,AE=AM=AD,∠CAE=∠CAM=∠BAD,推出∠DAM=∠BAC=60![]() ,则△ADM是等边三角形,得出DM=AD,易证AB>DM,AD>DC,得出△ABD与△DCM不全等,由折叠的性质得AE=AM,CE=CM,则AC垂直平分EM,即∠ENC=90
,则△ADM是等边三角形,得出DM=AD,易证AB>DM,AD>DC,得出△ABD与△DCM不全等,由折叠的性质得AE=AM,CE=CM,则AC垂直平分EM,即∠ENC=90![]() ,由∠ACE=60
,由∠ACE=60![]() ,得出∠CEN=30
,得出∠CEN=30![]() ,即可得出CN=
,即可得出CN=![]() EC.
EC.
解:∵△ABC是等边三角形,
∴AB=AC,∠B=∠BAC=∠ACE=60![]() ,
,
在△ABD和△ACE中,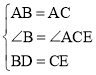 ,
,
∴△ABD≌△ACE(SAS),
∴∠BAD=∠CAE,AD=AE,故①正确;
由折叠的性质得:CE=CM=BD,AE=AM=AD,∠CAE=∠CAM=∠BAD,
∴∠DAM=∠BAC=60![]() ,
,
∴△ADM是等边三角形,
∴DM=AD,
∵AB>AD,
∴AB>DM,
∵∠ACD>∠DAC,
∴AD>DC,
∴△ABD与△DCM不全等,故③正确、②错误;
由折叠的性质得:AE=AM,CE=CM,
∴AC垂直平分EM,
∴∠ENC=90![]() ,
,
∵∠ACE=60![]() ,
,
∴∠CEN=30![]() ,
,
∴CN=![]() EC,故④正确,
EC,故④正确,
故答案为:①③④.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
图形的变化 | 示例图形 | 与对应线段有关的结论 | 与对应点有关的结论 |
平移 |
| (1)__________. |
|
轴对称 |
| (2)__________. | (3)__________. |
旋转 |
|
| (4)__________. |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

查看答案和解析>>
科目:初中数学 来源: 题型:
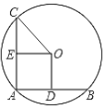
【题目】如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,则下列说法中正确的有( )
①点C、O、B一定在一条直线上;②若点E、点D分别是CA、AB的中点,则OE=OD;③若点E是CA的中点,连接CO,则△CEO是等腰直角三角形.
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.

(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
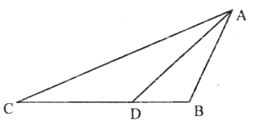
【题目】已知,如图△ABC中,AB=4,BC=8,D为BC边上的一点,BD=2.
(1)求证:△ABD∽△CBA;
(2)若DE∥AB交AC于点E,请你补全图形,再找出一个和△ABD相似的三角形,并计算DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
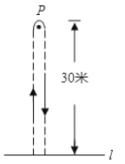
【题目】甲、乙两同学玩“托球赛跑”游戏,商定:用球拍托乒乓球从起跑线1起跑,绕过![]() 点跑回到起跑线(如图示),途中乒乓球掉下来时须捡起并回到掉球处继续赛跑,结果:甲同学由于心急,掉了球,浪费了6秒钟,乙同学则顺利跑完;事后,甲同学说:“我俩所用的全部时间的和为50秒”,乙同学说“捡球过程不算在内时,甲的速度是我的1.2倍”根据图文信息,求出两人所用的时间.
点跑回到起跑线(如图示),途中乒乓球掉下来时须捡起并回到掉球处继续赛跑,结果:甲同学由于心急,掉了球,浪费了6秒钟,乙同学则顺利跑完;事后,甲同学说:“我俩所用的全部时间的和为50秒”,乙同学说“捡球过程不算在内时,甲的速度是我的1.2倍”根据图文信息,求出两人所用的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com