
����Ŀ����ͼ�٣���ƽ��ֱ������ϵ�У�������y��ax2��bx��c��a��0��������D��2��4������x�ύ��A��B���㣬��y�ύ�ڵ�C��0��4��������AC��CD��BC�� ����AC=5��
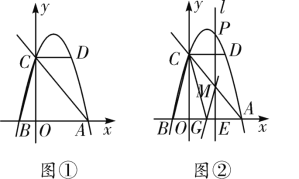
��1���������ߵĽ���ʽ��
��2����ͼ�ڣ���P���������ϵ�һ�����㣬����P��x��Ĵ���l��l�ֱ�x���ڵ�E����ֱ��AC�ڵ�M�����P�ĺ�����Ϊm����0<m��2ʱ������M��MG��BC��MG��x���ڵ�G������GC����mΪ��ֵʱ����GMC�����ȡ�����ֵ�������������ֵ��
��3����-1<m��2ʱ���Ƿ����ʵ��m��ʹ����P��C��MΪ����������κ͡�AEM���ƣ������ڣ������Ӧm��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��y=��![]() x2+
x2+![]() x+4����2����m=
x+4����2����m=![]() ʱ��S���S���=2����3��2��
ʱ��S���S���=2����3��2��![]()
��������
��1����ͨ�����ɶ�����ĵ�A�����꣬��A��C��D����������뼴����������ߵĽ���ʽ��
��2����A��C��������ֱ��AC����ʽ������m��ʾ����M���꣬��ʾ��ME�����ɡ�BCO�ס�GME�ɱ�ʾ��GE�����OG������������ĺͲ�ɵõ���GMC����������ö��κ��������ʿ���������ֵ��
��3���֡�CPM��90��͡�PCM��90���������������CPM��90��ʱ���ɵ�PC��x�ᣬ�������P�������m��ֵ������PCM��90��ʱ����PC��x���ڵ�F�����������������ε����������F�����꣬�����ֱ��CF�Ľ���ʽ�������������߽���ʽ�����P���������Ӧ��m��ֵ��
�⣨1���ߵ�C��0��4����
��OC��4��
��AC��5��
����Rt��AOC����AOC��90��
OA��![]()
�� A��3��0��
��A��3��0����C��0��4��D��2��4������������y��ax2��bx��c��a��0����
�� ��
��
��ã�
�������߽���ʽΪy����![]() x2��
x2��![]() x��4��
x��4��
��2����A��3��0����C��0��4���ɵ�ֱ��AC����ʽΪy����![]() x��4��
x��4��
��M������m����![]() m��4����
m��4����
��MG��BC��
���CBO����MGE������COB����MEG��90����
���BCO�ס�GME��
��![]() ����
����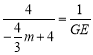 ��
��
��GE����![]() m��1��
m��1��
��OG��OE��GE��![]() m��1
m��1
��![]()
![]()
![]()
![]() ��
��
����m��![]() ʱ��S���S�����2��
ʱ��S���S�����2��
��3�����������֪��AEM��ֱ�������Σ�����MPC�У���PMC����AMEΪ��ǣ�
���PCM��ֱ�Ƕ��������P��C��
��һ�����������CMPM��90��ʱ����ͼ��
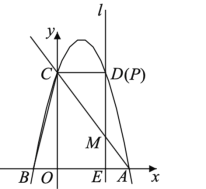
��CP��x�ᣬ��ʱ��P���D�غϣ�
����P��2��4������ʱm��2��
�ڶ������������PCM��90��ʱ����ͼ��
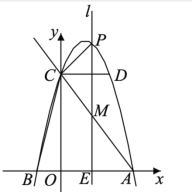
��ͼ���ӳ�PC��x���ڵ�F������FCA�ס�COA����![]() ��
��
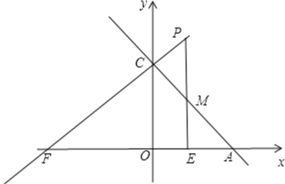
��AF��![]() ��
��
��OF��![]() ��
��
��F����![]() ��0����
��0����
��ֱ��CF�Ľ���ʽΪy��![]() x��4��
x��4��
����ֱ��CF�������߽���ʽ�ɵ�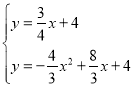 ��
��
��� ��
��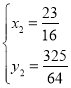 ��
��
��P������![]() ��
��![]() ������ʱm��
������ʱm��![]() ��
��
���Ͽ�֪��������������ʵ��m����ֵΪ2��![]()


 ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д� �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д� С����ȫ�ܼ��ϵ�д�
С����ȫ�ܼ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ����
����![]() �ӵ�
�ӵ�![]() ������
������![]() ���
���![]() �˶�����
�˶�����![]() �ӵ�
�ӵ�![]() ������
������![]() ���
���![]() �˶�����
�˶�����![]() �͵�
�͵�![]() ͬʱ�������ٶ���ͬ������
ͬʱ�������ٶ���ͬ������![]() ���
���![]() ����˶�ֹͣ��
����˶�ֹͣ��
��1����֤��![]() ��
��
��2����![]() ����
����![]() �Ķ�����
�Ķ�����
��3����![]() �����������ڲ�ʱ��ֱ��д��
�����������ڲ�ʱ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪y����x�Ķ��κ���y=x-bx+![]() b+b-5��ͼ����x�������������㣮
b+b-5��ͼ����x�������������㣮
��1����b��ȡֵ��Χ��
��2����bȡ�����������������ֵ����m��x��![]() ʱ������y��ȡֵ��Χ��n��y��6-2m����m��n��ֵ��
ʱ������y��ȡֵ��Χ��n��y��6-2m����m��n��ֵ��
��3�������Ա���x��ֵ����b��x��b+3������£���Ӧ����y����СֵΪ![]() �����ʱ���κ����Ľ���ʽ��
�����ʱ���κ����Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������֤����
��ͼ1����E��F�ֱ���������ABCD�ı�BC��CD�ϣ���EAF=45�������ж�BE��EF��FD֮���������ϵ��
С�ϰ���ABE�Ƶ�A��ʱ����ת90������ADG��ͨ��֤����AEF�ա�AGF���Ӷ����ֲ�֤����EF=BE+FD��
��������
��1����ͼ2����E��F�ֱ���������ABCD�ı�CB��CD���ӳ����ϣ���EAF=45��������EF�������С�ϵķ��ָ������ʾд��EF��BE��DF֮���������ϵ����֤����
��������չ��
��2����ͼ3����ͼ����BAC=90����AB=AC����E��F�ڱ�BC�ϣ��ҡ�EAF=45������BE=3��EF=5����CF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
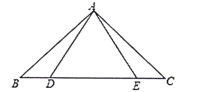
����Ŀ��Ϊ�˽�ijУ���꼶����1000���ܵ�ˮƽ�����������ȡ�����������в��ԣ����Ѳ��Գɼ���ΪD��C��B��A�ĸ��ȴλ��Ƴ���ͼ��ʾ�IJ�������ͳ��ͼ��������ͼ����������⣺
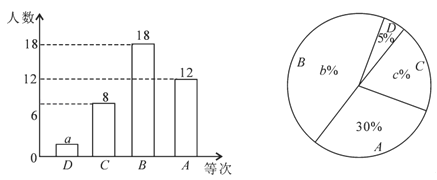
��1��a=�� ����b=�� ����c=�� ����
��2������ͳ��ͼ�б�ʾC�ȴε��������Ե�Բ�ĽǵĶ���Ϊ�� ���ȣ�
��3��ѧУ������A�ȴεļס��ҡ����������������У����ѡȡ���������μ�ȫ����ѧ��1000���ܱ����������б�������״ͼ������ס�����������ͬʱ��ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ 3 �� 12 ��ֲ�����ڼ䣬 ѧУԤ���� A��B �������磬������ A������ 3 �ã�B ������ 5 �ã��� 2100 Ԫ�������� A ������ 4 �ã�B ������ 10�ã��� 3800 Ԫ��
��1���� A��B ��������ĵ��ۣ�
��2�����õ�λ���ò����� 8000 Ԫ��Ǯ�������������繲 30 �ã��� A �����������蹺�����ٿã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC������ABC����BC����ƽ�Ƶõ���DEF�����е�E�ڱ�BC�ϣ�DE��AC�ཻ�ڵ�O������AE��DC��AD������E��ʲôλ��ʱ���ı���AECDΪ���Σ���˵�����ɣ�
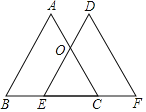
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����CΪ��O��һ�㣬AD��CD������D�ڡ�O�⣩ACƽ�֡�BAD��

��1����֤��CD�ǡ�O�����ߣ�
��2����DC��AB���ӳ����ཻ�ڵ�E����DE��12��AD��9����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
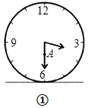
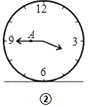
����Ŀ��ͼ�ٱ�ʾһ��ʱ�ӵ����洹ֱ�̶���ˮƽ�����ϣ����з�������һ��![]() ����������ʾ3��30��ʱ�����봹ֱ�����棬��
����������ʾ3��30��ʱ�����봹ֱ�����棬��![]() ��������ĸ߶�Ϊ
��������ĸ߶�Ϊ![]() ���֣�ͼ�ڱ�ʾ������ʾ3��45ʱ����
���֣�ͼ�ڱ�ʾ������ʾ3��45ʱ����![]() ������ĸ߶�Ϊ
������ĸ߶�Ϊ![]() ���֣���������ʾ3��55ʱ����
���֣���������ʾ3��55ʱ����![]() ��������ĸ߶�Ϊ__________���֣�
��������ĸ߶�Ϊ__________���֣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com