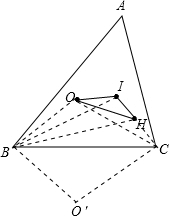
解:△ABC的外接圆与△IOH的外接圆的大小相等.
理由:作O关于BC的对称点O′,连接BO、BI、BH、BO′、CO、CI、CH、CO′,
(1)由三角形外心、内心、垂心的张角公式可知,
∠BOC=2∠A=120°,
∠BIC=90°+

∠A=120°,∠BHC=180°-∠A=120°,
则B、C、H、I、O五点共圆,即△IOH的外接圆与△OBC的外接圆是同一个圆;
(2)由轴对称可知∠BO′C=∠BOC=120°,
∠A+∠BO′C=180°,
则A、B、O′、C四点共圆,即△O′BC的外接圆与△ABC的外接圆是同一个圆;
(3)由对称性可证△OBC≌△O′BC,即△OBC的外接圆与△O′BC的外接圆相等;
由(1)-(3)得△ABC的外接圆与△IOH的外接圆相等.
分析:(1)由三角形外心、内心、垂心的张角公式可求∠BOC=∠BIC=∠BHC=120°,可证B、C、H、I、O五点共圆,即△IOH的外接圆与△OBC的外接圆是同一个圆;
(2)由轴对称可知∠BO′C=∠BOC=120°,则∠A+∠BO′C=180°,可证A、B、O′、C四点共圆,即△O′BC的外接圆与△ABC的外接圆是同一个圆;
(3)由对称性可证△OBC≌△O′BC,即△OBC的外接圆与△O′BC的外接圆相等;
综合(1)(2)(3)可证本题结论.
点评:本题考查了三角形外心、内心、垂心的性质.关键是根据题意找出四点共圆,五点共圆,判断三角形共圆,利用“传递”的方法证明本题结论.

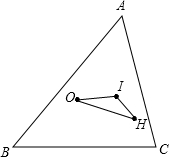 如图,在△ABC中,∠A=60°,O,I,H分别是它的外心,内心,垂心.试比较△ABC的外接圆与△IOH的外接圆的大小,证明你的论断.
如图,在△ABC中,∠A=60°,O,I,H分别是它的外心,内心,垂心.试比较△ABC的外接圆与△IOH的外接圆的大小,证明你的论断. 解:△ABC的外接圆与△IOH的外接圆的大小相等.
解:△ABC的外接圆与△IOH的外接圆的大小相等. ∠A=120°,∠BHC=180°-∠A=120°,
∠A=120°,∠BHC=180°-∠A=120°,

 备战中考寒假系列答案
备战中考寒假系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为