
����Ŀ����12�֣��Ķ����ϣ�
��ͼ1����ƽ��֮������ϵxOy�У�A��B���������ֱ�ΪA��x1��y1����B��x2��y2�����ɹ��ɶ�����AB2=|x2��x1|2+|y2��y1|2������A��B�����ľ���ΪAB=![]() ��
��
����֪����Բ���Կ��ɵ�Բ�ľ�����ڰ뾶�ĵ�ļ��ϣ���ͼ2����ƽ��ֱ������ϵxoy�У�A��x��y��ΪԲ������һ�㣬��A��ԭ��ľ����ƽ��ΪOA2=|x��0|2+|y��0|2������O�İ뾶Ϊrʱ����O�ķ��̿�дΪ��x2+y2=r2��
������չ�����Բ������ΪP��a��b�����뾶Ϊr����ô��P�ķ��̿���дΪ ��
�ۺ�Ӧ�ã�
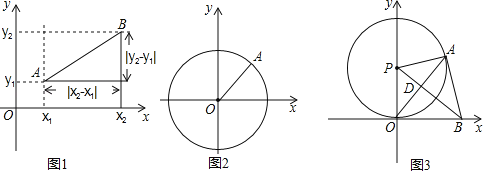
��ͼ3����P��x��������ԭ��O��P������Ϊ��0��6����A����P��һ�㣬����OA��ʹtan��POA=![]() ����PD��OA������ΪD���ӳ�PD��x���ڵ�B������AB��
����PD��OA������ΪD���ӳ�PD��x���ڵ�B������AB��
��֤��AB����P���е㣻
���Ƿ���ڵ��ĵ�O��P��A��B���붼��ȵĵ�Q�������ڣ���Q�����꣬��д����QΪԲ�ģ���OQΪ�뾶����O�ķ��̣��������ڣ�˵��������
���𰸡�������չ����x��a��2+��y��b��2=r2�ۺ�Ӧ�ã�������������Q������Ϊ��4��3��������Ϊ��x��4��2+��y��3��2=25��
��������
����������չ����A��x��y��Ϊ��P������һ�㣬����AP=r�������Ķ������е�����֮����빫ʽ���������P�ķ��̣�
�ۺ�Ӧ�ã�����PO=PA��PD��OA�ɵ���OPD=��APD���Ӷ���֤����POB�ա�PAB��������POB=��PAB������P��x��������ԭ��O�ɵ���POB=90�㣬���ɵõ���PAB=90�㣬�ɴ˿ɵ�AB����P�����ߣ�
������Q���߶�BP�е�ʱ������ֱ��������б���ϵ����ߵ���б�ߵ�һ��ɵ�QO=QP=BQ=AQ����֤��OBP=��POA������tan��OBP=![]() =
=![]() ����P����������OP��OB������Q��QH��OB��H����֤��BHQ�ס�BOP���������������ε����ʿ����QH��BH���������OH���Ϳɵõ���Q�����꣬Ȼ������������չ�еĽ��۾Ϳɽ��������
����P����������OP��OB������Q��QH��OB��H����֤��BHQ�ס�BOP���������������ε����ʿ����QH��BH���������OH���Ϳɵõ���Q�����꣬Ȼ������������չ�еĽ��۾Ϳɽ��������
����������⣺������չ����A��x��y��Ϊ��P������һ�㣬
��P��a��b�����뾶Ϊr��
��AP2=��x��a��2+��y��b��2=r2��
�ʴ�Ϊ��x��a��2+��y��b��2=r2��
�ۺ�Ӧ�ã�
�١�PO=PA��PD��OA��
���OPD=��APD��
����POB����PAB��
 ��
��
���POB�ա�PAB��
���POB=��PAB��
�ߡ�P��x��������ԭ��O��
���POB=90�㣬
���PAB=90�㣬
��AB����P�����ߣ�
�����ڵ��ĵ�O��P��A��B���붼��ȵĵ�Q��
����Q���߶�BP�е�ʱ��
�ߡ�POB=��PAB=90�㣬
��QO=QP=BQ=AQ��
��ʱ��Q���ĵ�O��P��A��B���붼�����
�ߡ�POB=90�㣬OA��PB��
���OBP=90�㩁��DOB=��POA��
��tan��OBP=![]() =tan��POA=
=tan��POA=![]() ��
��
��P��������0��6����
��OP=6��OB=![]() OP=8��
OP=8��
����Q��QH��OB��H����ͼ3��
������QHB=��POB=90�㣬
��QH��PO��
���BHQ�ס�BOP��
��![]() =
=![]() =
=![]() =
=![]() ��
��
��QH=![]() OP=3��BH=
OP=3��BH=![]() OB=4��
OB=4��
��OH=8��4=4��
����Q��������4��3����
��OQ=![]() =5��
=5��
����QΪԲ�ģ���OQΪ�뾶����O�ķ���Ϊ��x��4��2+��y��3��2=25��


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
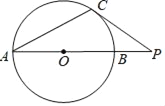
����Ŀ����ͼ��C�ǡ�O��һ�㣬��P��ֱ��AB���ӳ����ϣ���O�İ뾶Ϊ3��PB=2��PC=4��
��1����֤��PC�ǡ�O�����ߣ�
��2����tan��CAB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B���ر�����������С��ͨ�����з��������A��B��ľ��룺����AB��ѡһ��C��Ȼ����AC��BC���е�M��N����������MN�ij�Ϊ12m���ɴ�����֪����A��B��ľ��룮�й������̽������������������ ��
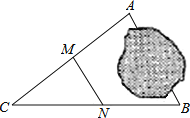
A. AB=24m B. MN��AB
C. ��CMN�ס�CAB D. CM��MA=1��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCO�У�O��0��0����C��0��3����A��a��0������a��3������AΪ��ת����˳ʱ����ת����ABCO�õ�����AFED��
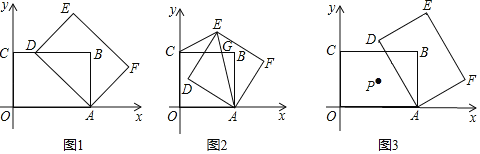
��1����ͼ1������D���ڱ�BC��ʱ����BD�ij�����a��ʽ�ӱ�ʾ����
��2����ͼ2����a��3ʱ������AFED�ĶԽ���AE������ABCO�ı�BC�ڵ�G������CE������CGE�ǵ��������Σ���ֱ��BE�Ľ���ʽ��
��3����ͼ3������ABCO�ĶԳ�����Ϊ��P����P��B����AD�Գ�ʱ�����a��ֵ����ʱ��x�ᡢy�����Ƿ�ֱ����M��Nʹ���ı���EFMNΪƽ���ı��Σ�������ֱ��д��M��N���꣬������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y��ax2��bx��c(a��0)ͼ���һ���֣��Գ���Ϊֱ��x��![]() ���Ҿ�����(2��0)������˵������abc��0����a��b��0����4a��2b��c��0������(��2��y1)��(
���Ҿ�����(2��0)������˵������abc��0����a��b��0����4a��2b��c��0������(��2��y1)��(![]() ��y2)���������ϵ����㣬��y1��y2.����˵����ȷ����( )
��y2)���������ϵ����㣬��y1��y2.����˵����ȷ����( )
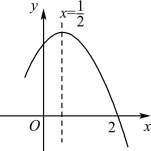
A. �ڢۢ� B. �٢ڢ� C. �٢� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ⲻ��ʽ�飺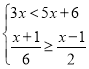 ��
��
��2����ʽ�ֽ⣺��x��2����x��8��+8��
��3���ⷽ�̣�![]() +
+![]() ��
��![]() ��
��
��4���ⷽ�̣���2x��1��2��3��6x��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABΪ��O��ֱ�����ӳ�AB����P������P��ԲO�����ߣ��е�ΪC������AC����AC=CP.
��1�����P�Ķ�����
��2������D�ǻ�AB���е㣬����CD��AB�ڵ�E����DE��DC=20�����O�����.����ȡ3.14��
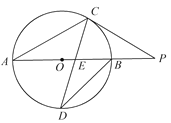
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ�С���ͬѧΪ������˸߶ȣ����ƶ������²���������ʹ�ù����Dz���Ǻ�Ƥ�ߣ�������鳤��ƽ��ɷ������ݣ��ú�a��b�����Ĵ���ʽ��ʾ���AB�ĸ߶ȣ�
��ѧ�����
�ʱ�䣺2018��4��2�� ��ص㣺ѧУ�ٳ� ����ˣ���ƽ
���� | ����ѧУ��˵ĸ߶� | ||
�Ŀ�� | ������ѧ��ѧ֪ʶ���������ʵ������ | ||
����ʾ��ͼ |
| �������� | ��1����ʲô��á�ADE=���� ��2����ʲô���BC=a�ף�CD=b�ף� |
��3��������� | |||
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ǿ����������صı�����ʽ.��������У���������������������Ը�Ʒ�ʣ�������ɫ������.������������Ĺ�ֱ����������ǿ������.�������Ų����Ŀ�Ƭ���������ſ�Ƭ������ͼ��Ϊ��������������һ�ſ�Ƭ������ͼ��Ϊ������������Ƭ������ͼ����ͬ�⣬�������ͬ���������ſ�Ƭ��������ϴ�ȣ����������ȡһ�ţ���¼ͼ�����Ż�������ϴ�Ⱥ��ٴ��������ȡһ�ţ�
���û���״ͼ���б��ķ��������������ſ�Ƭ�ϵ�ͼ�����ǡ��������ĸ��ʣ���ͼ��Ϊ�������������ſ�Ƭ�ֱ��ΪA1��A2��ͼ��Ϊ���������Ŀ�Ƭ��ΪB��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com