
【题目】甲、乙两名同学进行登山比赛,图中表示甲同学和乙同学沿相同的路线同时从山脚出发到达山顶过程中,各自行进的路程随时间变化的图象,根据图象中的有关数据回答下列问题:

(1)分别求出表示甲、乙两同学登山过程中路程![]() (千米)与时间
(千米)与时间![]() (时)的函数解析式;(不要求写出自变量
(时)的函数解析式;(不要求写出自变量![]() 的取值范围)
的取值范围)
(2)当甲到达山顶时,乙行进到山路上的某点![]() 处,求
处,求![]() 点距山顶的距离;
点距山顶的距离;
(3)在(2)的条件下,设乙同学从![]() 处继续登山,甲同学到达山顶后休息1小时,沿原路下山,在点
处继续登山,甲同学到达山顶后休息1小时,沿原路下山,在点![]() 处与乙相遇,此时点
处与乙相遇,此时点![]() 与山顶距离为1.5千米,相遇后甲、乙各自按原来的路线下山和上山,求乙到达山顶时,甲离山脚的距离是多少千米?
与山顶距离为1.5千米,相遇后甲、乙各自按原来的路线下山和上山,求乙到达山顶时,甲离山脚的距离是多少千米?
【答案】(1)S甲=3t,S乙=2t;(2)4千米;(3)甲距山脚6千米.
【解析】
(1)由图可知,甲、乙两同学登山过程中路程s与时间t都成正比例函数,分别设为S甲=k1t,S乙=k2t,用待定系数法可求解;
(2)由图可知,甲到达山顶时路程为12千米,即山脚到山顶的距离为12千米,代入S甲可求得所花的时间,再把时间代入S乙即可求得A点离山脚的距离,则A点与山顶的距离可求;
(3)由图象知:甲到达山顶并休息1小时后点D的坐标为(5,12),点B的坐标也可求,则线段DF所在直线的一次函数表达式可求,而乙到达山顶的时间可求,则题目可求解.
解:(1)设甲、乙两同学登山过程中,路程s(千米)与时间t(时)的函数解析式分别为
S甲=k1t,S乙=k2t
由题意,得6=2k1,6=3k2
∴k1=3,k2=2
∴解析式分别为S甲=3t,S乙=2t;
(2)甲到达山顶时,由图象可知,当S甲=12千米,代入S甲=3t得t=4(小时)
∴S乙=2×4=8(千米)
∴128=4(千米)
答:当甲到达山顶时,乙距山顶的距离为4千米.
(3)由图象知:甲到达山顶并休息1小时后点D的坐标为(5,12)
由题意,得:点B的纵坐标为12![]() =
=![]() ,代入S乙=2t,
,代入S乙=2t,
解得:t=![]() ,
,
∴点B(![]() ,
,![]() )
)
设过B、D两点的直线解析式为S=kt+b,
由题意,得: ,
,
解得![]() ,
,
∴直线BD的解析式为S=6t+42
当乙到达山顶时,S乙=12,得t=6,把t=6代入S=6t+42得S=6(千米).
答:乙到达山顶时,甲距山脚6千米.


科目:初中数学 来源: 题型:
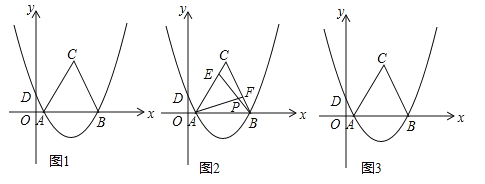
【题目】如图1,抛物线![]() ,经过A(1,0)、B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边△ABC.
,经过A(1,0)、B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边△ABC.
(1)求抛物线的解析式;
(2)在x轴上方的抛物线上是否存在点M,是S△ABM=![]() S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)如图2,E是线段AC上的动点,F是线段BC上的动点,AF与BE相交于点P.
①若CE=BF,试猜想AF与BE的数量关系及∠APB的度数,并说明理由;
②若AF=BE,当点E由A运动到C时,请直接写出点P经过的路径长(不需要写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
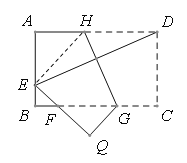
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上E处,EQ与BC相交于F,若AD=8 cm,AB=6 cm,AE=4cm,则△EBF的周长是______________ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售![]() 、
、![]() 两种品牌的洗衣机,进价及售价如下表:
两种品牌的洗衣机,进价及售价如下表:
品牌 |
|
|
进价(元/台) | 1500 | 1800 |
售价(元/台) | 1800 | 2200 |
(1)该商场9月份用45000元购进![]() 、
、![]() 两种品牌的洗衣机,全部售完后获利9600元,求商场9月份购进
两种品牌的洗衣机,全部售完后获利9600元,求商场9月份购进![]() 、
、![]() 两种洗衣机的数量;
两种洗衣机的数量;
(2)该商场10月份又购进![]() 、
、![]() 两种品牌的洗衣机共用去36000元
两种品牌的洗衣机共用去36000元
①问该商场共有几种进货方案?请你把所有方案列出来;
②通过计算说明洗衣机全部销售完后哪种进货方案所获得的利润最大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算;
(1)23=_____;
(2)﹣2+|﹣2|=_____;
(3)﹣6×(﹣16)=_____;
(4)![]() =_____;
=_____;
(5)2a+a=_____;
(6)![]() =_____;
=_____;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,在数轴上,点M,N分别表示数m,n则点M,N之间的距离为|m﹣n|.已知点A,B,C,D在数轴上分别表示数a,b,c,d,且|a﹣c|=|b﹣c|=![]() |d﹣a|=1(a≠b),则线段BD的长度为_____.
|d﹣a|=1(a≠b),则线段BD的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线:y=ax2+bx+c(a<0)经过A(2,4)、B(﹣1,1)两点,顶点坐标为(h,k),则下列正确结论的序号是( )
①b>1;②c>2;③h>![]() ;④k≤1.
;④k≤1.
A. ①②③④ B. ①②③ C. ①②④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com