
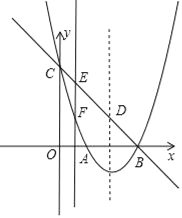
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,﹣1),图象与y轴交于点C(0,3),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)设抛物线对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
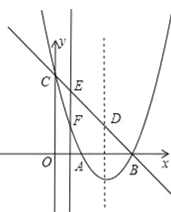
(3)点E为直线BC上的任意一点,过点E作x轴的垂线与抛物线交于点F,问是否存在点E使△DEF为直角三角形?若存在,求出点E坐标,若不存在,请说明理由.
【答案】(1)抛物线解析式为y=x2﹣4x+3;(2)S△ACD=2;(3)存在满足条件的点E,其坐标为(2+![]() ,1﹣
,1﹣![]() )或(2﹣
)或(2﹣![]() ,1+
,1+![]() )或(1,2)或(4,﹣1).
)或(1,2)或(4,﹣1).
【解析】试题分析:(1)设顶点式y=a(x-2)2-1(a≠0),然后把C点坐标代入求出a即可;
(2)通过解方程x2-4x+3=0得A(1,0),B(3,0),再利用待定系数法求出直线BC解析式为y=-x+3,从而得到D(2,1),然后利用S△ACD=S△ABC-S△ABD进行计算即可;
(3)易得∠FED≠90°,则△DEF为直角三角形,分∠DFE=90°和∠EDF=90°两种情况,①当∠DFE=90°时F点纵坐标为1,解方程x2-4x+3=1得点E的横坐标为2±![]() ,再利用点E在直线y=-x+3上可确定E点坐标;②当∠EDF=90°时,先确定直线AD解析式为y=x-1,则可判断AD⊥BC,所以直线AD与抛物线的交点即为E点,解方程x2-4x+3=x-1得E点的横坐标,然后利用直线BC的解析式确定E点坐标.
,再利用点E在直线y=-x+3上可确定E点坐标;②当∠EDF=90°时,先确定直线AD解析式为y=x-1,则可判断AD⊥BC,所以直线AD与抛物线的交点即为E点,解方程x2-4x+3=x-1得E点的横坐标,然后利用直线BC的解析式确定E点坐标.
(1)∵抛物线的顶点坐标为(2,﹣1),
∴可设抛物线解析式为y=a(x﹣2)2﹣1(a≠0),
把C(0,3)代入可得a(0﹣2)2﹣1=3,解得a=1,
∴抛物线解析式为y=(x﹣2)2﹣1,即y=x2﹣4x+3;
(2)在y=x2﹣4x+3中,令y=0可得x2﹣4x+3=0,解得x=1或x=3,
∴A(1,0),B(3,0),
设直线BC解析式为y=kx+3,把B(3,0)代入得:3k+3=0,解得k=﹣1,
∴直线BC解析式为y=﹣x+3,
由(1)可知抛物线的对称轴为x=2,此时y=﹣x+3=1,
∴D(2,1),
∴S△ACD=S△ABC﹣S△ABD=![]() ×2×3﹣
×2×3﹣![]() ×2×1=2;
×2×1=2;
(3)由题意知EF∥y轴,则∠FED=∠OCB≠90°,
∴△DEF为直角三角形,分∠DFE=90°和∠EDF=90°两种情况,
①当∠DFE=90°时,即DF∥x轴,则D、F的纵坐标相同,
∴F点纵坐标为1,
∵点F在抛物线上,
∴x2﹣4x+3=1,解得x=2±![]() ,即点E的横坐标为2±
,即点E的横坐标为2±![]() ,
,
∵点E在直线y=﹣x+3上,
∴当x=2+![]() 时,y=﹣x+3=1﹣
时,y=﹣x+3=1﹣![]() ;
;
当x=2﹣![]() 时,y=﹣x+3=1+
时,y=﹣x+3=1+![]() ,
,
∴E点坐标为(2+![]() ,1﹣
,1﹣![]() )或(2﹣
)或(2﹣![]() ,1+
,1+![]() );
);
②当∠EDF=90°时,
∵A(1,0),D(2,1),
∴直线AD解析式为y=x﹣1,
∵直线BC解析式为y=﹣x+3,
∴AD⊥BC,
∴直线AD与抛物线的交点即为E点,
联立直线AD与抛物线解析式有x2﹣4x+3=x﹣1,解得x=1或x=4,
当x=1时,y=﹣x+3=2;当x=4时,y=﹣x+3=﹣1,
∴E点坐标为(1,2)或(4,﹣1),
综上所述,存在满足条件的点E,其坐标为(2+![]() ,1﹣
,1﹣![]() )或(2﹣
)或(2﹣![]() ,1+
,1+![]() )或(1,2)或(4,﹣1).
)或(1,2)或(4,﹣1).


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分
组别 |
|
|
|
|
|
正确字数 |
|
|
|
|
|
人数 | 10 | 15 | 25 |
|
|

根据以上信息解决下列问题:
![]() ,
,![]() ,并补全条形统计图.
,并补全条形统计图.
(2)扇形统计图中“![]() 组”所对应的圆心角的度数是 .
组”所对应的圆心角的度数是 .
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长度为4π.
(1)求证:DE∥BC;
(2)若AF=CE,求线段BC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,连接AD.
(1)若∠BAD=45°,求证:△ACD为等腰三角形;
(2)若△ACD为直角三角形,求∠BAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人共同计算一道整式乘法:(2x+a)(3x+b),由于甲抄错了第一个多项式中a的符号,得到的结果为6x2+11x-10;由于乙漏抄了第二个多项式中的x的系数,得到的结果为2x2-9x+10.请你计算出a,b的值各是多少,并写出这道整式乘法的正确结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=8,BO=DO=6,点P为线段AC上的一个动点。

⑴ 填空:AD=CD=_____ .
⑵ 过点P分别作PM⊥AD于M点,作PH⊥DC于H点.连结PB,在点P运动过程中,PM+PH+PB的最小值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
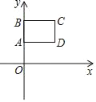
【题目】如图,在平面直角坐标系中,长方形ABCD的边AB在y轴正半轴上,顶点A的坐标为(0,2),设顶点C的坐标为(a,b).
(1)顶点B的坐标为 ,顶点D的坐标为 (用a或b表示);
(2)如果将一个点的横坐标作为x的值,纵坐标作为y的值,代入方程2x+3y=12成立,就说这个点的坐标是方程2x+3y=12的解.已知顶点B和D的坐标都是方程2x+3y=12的解,求a,b的值;
(3)在(2)的条件下,平移长方形ABCD,使点B移动到点D,得到新的长方形EDFG,
①这次平移可以看成是先将长方形ABCD向右平移 个单位长度,再向下平移 个单位长度的两次平移;
②若点P(m,n)是对角线BD上的一点,且点P的坐标是方程2x+3y=12的解,试说明平移后点P的对应点P′的坐标也是方程2x+3y=12的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com