练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在□ABCD中，对角线AC,BD交于点O，AC＝8，BD=12,则AD的取值范围是___________________.

    【答案】2<AD<10

    【解析】由对角线的性质可得，AC=2OA，BD=2OD，所以OA=4，OD=6，则6-4＜AD＜6+4，即2＜AD＜10，故答案为2＜AD＜10.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】|－1|是数轴上表示________的点到原点的距离

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点D、E分别是边BC、AC的中点，过点A作AF∥BC交DE的延长线于F点，连接AD、CF．

    （1）求证：四边形ADCF是平行四边形；
    （2）当△ABC满足什么条件时，四边形ADCF是菱形？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：
    （1）（﹣）2014×（1.5）2015﹣20140；
    （2）（x+y）2﹣（x﹣y）（x+y）；
    （3）[x（x2y2+xy）﹣y（x2﹣x3y）]÷3x2y；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，DE垂直平分AB，分别交AB、AC于点D、E，若∠EBC=30°，则∠A=（ ）

    A.30°
    B.35°
    C.40°
    D.45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

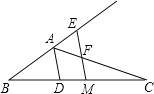
    【题目】（8分）如图，已知△ABC，AD平分∠BAC交BC于点D，BC的中点为M，ME∥AD，交BA的延长线于点E，交AC于点F．

    （1）求证：AE=AF；

    （2）求证：BE=（AB+AC）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB＝6，O是AB的中点，直线l经过点O，∠1＝120°，P是直线l上一点。当△APB为直角三角形时，AP＝ .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们对多项式x+x﹣6进行因式分解时，可以用特定系数法求解．例如，我们可以先设x2+x﹣6=（x+a）（x+b），显然这是一个恒等式．根据多项式乘法将等式右边展开有：x2+x﹣6=（x+a）（x+b）=x+（a+b）x+ab
    所以，根据等式两边对应项的系数相等，可得：a+b=1，ab=﹣6，解得a=3，b=﹣2或者a=﹣2，b=3．所以x2+x﹣6=（x+3）（x﹣2）．当然这也说明多项式x2+x﹣6含有因式：x+3和x﹣2．
    像上面这种通过利用恒等式的性质来求未知数的方法叫特定系数法．利用上述材料及示例解决以下问题．
    （1）已知关于x的多项式x2+mx﹣15有一个因式为x﹣1，求m的值；
    （2）已知关于x的多项式2x3+5x2﹣x+b有一个因式为x+2，求b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在同一平面内，有三条直线a，b，c，若a∥b，b∥c，则直线a与直线c之间的位置关系是(　　)

    A. 相交

    B. 平行

    C. 垂直

    D. 平行或相交

    查看答案和解析>>

    同步练习册答案