
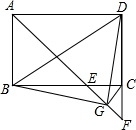
 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:分析 ①根据矩形的性质可得出∠BAD=∠ABC=90°,AB=CD,再由角平分线的性质可得出∠BAE=45°,通过角的计算即可得出∠BAE=∠BEA,从而得出AB=BE=CD,即①正确;②根据平行线的性质以及对顶角相等可得出△CEF为等腰直角三角形,由此得出∠CGF=90°,∠FCG=45°,根据三角形外角的性质可得出∠CGD<45°,再由角的关系即可得出∠DGF=∠CGD+∠CGF<135°,即②不正确;③通过角的计算可得出∠BEG=∠DCG,再根据等腰直角三角形的性质可得出CG=EG,由此即可利用全等三角形的判定定理(SAS)证出△BEG≌△DCG,即③正确;④由③可得出∠EBG=∠CDG,根据角的计算即可得出∠ABG+∠ADG=180°,即④正确;⑤过点G作GM⊥DF于点M,设AB=2a(a>0),则AD=3a,利用分割图形求面积法结合三角形的面积公式可算出S△BDG和S△DGF的值,由此可得出⑤正确.综上即可得出结论.
解答 解:①∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,AB=CD,
∵AE是∠BAD的角平分线,
∴∠BAE=∠DAE=45°,
∴∠AEB=90°-∠BAE=45°=∠BAE,
∴BE=AB=CD,①正确;
②∵AB∥CD,
∴∠CFE=∠BAE=45°,∠CEF=∠AEB=45°,
∴△CEF为等腰直角三角形,
∵点G为EF的中点,
∴CG⊥EF,∠CGF=90°,∠FCG=45°,
∵∠FCG=∠CGD+∠CDG=45°,
∴∠CGD<45°,
∴∠DGF=∠CGD+∠CGF<45°+90°=135°,②不正确;
③∵△CEF为等腰直角三角形,
∴CG=EG.
∵∠BEG=180°-∠CEF=135°,∠DCG=180°-∠FCG=135°,
∴∠BEG=∠DCG,
在△BEG和△DCG中,有$\left\{\begin{array}{l}{BE=DC}\\{∠BEG=∠DCG}\\{EG=CG}\end{array}\right.$,
∴△BEG≌△DCG(SAS),③正确;
④∵△BEG≌△DCG,
∴∠EBG=∠CDG,
∵∠ABG=∠ABC+∠EBG,∠ADG=∠ADC-∠CDG,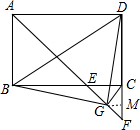
∴∠ABG+∠ADG=∠ABC+∠ADC=180°,④正确;
⑤过点G作GM⊥DF于点M,如图所示.
∵$\frac{AB}{AD}$=$\frac{2}{3}$,
∴设AB=2a(a>0),则AD=3a.
∵∠DAF=45°,∠ADF=90°,
∴△ADF为等腰直角三角形,
∴DF=AD=3a.
∵△CGF为等腰直角三角形,
∴GM=CM=$\frac{1}{2}$CF=$\frac{1}{2}$(DF-CD)=$\frac{1}{2}$a,
∴S△DGF=$\frac{1}{2}$DF•GM=$\frac{1}{2}$×3a×$\frac{1}{2}$a=$\frac{3}{4}{a}^{2}$.
S△BDG=S△BCD+S梯形BGMC-S△DGM=$\frac{1}{2}$×2a×3a+$\frac{1}{2}$×(3a+$\frac{1}{2}$a)×$\frac{1}{2}$a-$\frac{1}{2}$×$\frac{1}{2}$a×(2a+$\frac{1}{2}$a)=$\frac{13}{4}{a}^{2}$.
∴3S△BDG=13S△DGF,⑤正确.
综上可知:正确的结论有①③④⑤.
故答案为:①③④⑤.
点评 本题考查了矩形的性质、等腰直角三角形的判定及性质、全等三角形的判定及性质、三角形的面积公式以及角的计算,解题的关键是逐条分析5个结论是否正确.本题属于中档题,难度不大,但解题过程稍显繁琐,好在该题为填空题,好多结论可以直接拿来运用,不需去证明.解决该题型时,利用分割图形法求面积是难点,此处应该加以重视.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com